Question

How do you draw the graph for $y=-cotx$ for $0\le x\le 2\pi$ ?

Answer 1

First of all, we will see in which quadrant value of cotangent is positive and in which quadrant, it is negative. Then we can just reverse the quadrants for $-cot\text{ }x$ to check where positive values lie and where negative. Then we will plot the x-y graph, where the x-axis will represent the angle in radians while the y-axis will denote the value of the function. The value of $x$ lies between $0$ and $2\pi$ so the x-quadrant will contain an angle between them. The range of the function is $cotx<-1$ or $cotx>1$.
Then $-cotx>1$ or $-cotx\text{ }<-1$. This implies $y>1$ or $y<1$.

Complete step by step solution:
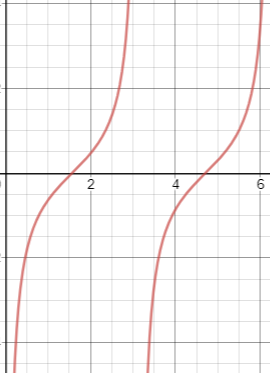
We have to plot the graph of $-cot\text{ }x$
For this we should have the value of $cot\text{ }x$ in the given domain $\left[ 0,2\pi \right]$.
We know that cot gives positive values in the first and fourth quadrant and negative values in the second and third quadrant.
So, -cot will give negative values in the first and fourth quadrant and positive values in the second and third quadrant.
The cycle changes after $\pi$ radians. So, there is one cycle between $0$ and $\pi$, another between $\pi$ and $2\pi$ and so on.
Every cycle has vertical asymptotes at the end of the cycle.
The value of cot in each cycle is decreasing so $-cot\text{ }x$ will have increasing values in each cycle.
So , keeping all these points in mind , we plot the following graph:

Note:
The asymptotes of $\text{cot }x$ are the x-intercepts of the function $\text{tan }x$. While the asymptotes of $\text{tan }x$ is the x-intercept of the function $\text{cot }x$.