Question

How do you do linear programming?

Answer 1

In this question, we have to find the steps of doing the linear programming. As we know, linear programming is a method to find the best possible outcome from linear relationships. Thus, to solve a linear program problem, it is given to us with objective functions and inequality constraints. Therefore, we will first take the equality sign of the constraints inequalities and solve for both the variables. Then, we will plot those equality equations in the graph. After that, we will find the constraint region by putting the value of the variables equal to 0 in the inequations. After that, we will shade the region and thus find the closed or open region. In the last, we will find the corner points of the feasibility region and put it in the objective function, to get the optimal solution of the problem.

Complete step-by-step answer:
According to the question, we have to solve the linear programming problem. As we know, a linear programming is the method to find the best optimal solution from linear relationships. Thus, to solve this problem, we will first let a programming linear function, that is
We have to find the maximal and minimal value for the objective function $z=5x+3y$ with the constraints $x+2y\le 14,3x-y\ge 0,x-y\le 2$ where both $x,y\ge 0$ .
So, the constraints given to us are:
$\begin{aligned} & x+2y\le 14 \\\ & 3x-y\ge 0 \\\ & x-y\le 2 \\\ \end{aligned}$
So, now we will first plot the above three inequations in the graph by taking the equality of all the three inequation, we get
$x+2y=14$ --------- (1)
$3x-y=0$ ----------- (2)
$x-y=2$ --------- (3)
Now, we will solve equation (1), by letting different values of y and solve for x, that is
Let us suppose $y=0$ . Now, we will put it in equation (1), we get
$\Rightarrow x+2.(0)=14$
On further solving, we get
$\Rightarrow x=14$
Let us suppose $y=1$ . Now, we will put it in equation (1), we get
$\Rightarrow x+2.(1)=14$
On further solving, we get
$\Rightarrow x+2=14$
Now, we will subtract 2 on both sides in the above equation, we get
$\Rightarrow x+2-2=14-2$
As we know, the same term with opposite signs cancel out each other, thus we get
$\Rightarrow x=12$
Therefore, the coordinates for the equation $x+2y=14$ are $\left( 14,0 \right),\left( 12,1 \right)$ ---- (4)
Similarly, we will solve equation (2), by letting different values of x and solve for y, that is
Let us suppose $x=0$ . Now, we will put it in equation (2), we get
$\Rightarrow 3.(0)-y=0$
On further solving, we get
$\Rightarrow y=0$
Let us suppose $x=1$ . Now, we will put it in equation (2), we get
$\Rightarrow 3(1)-y=0$
On further solving, we get
$\Rightarrow 3-y=0$
Now, we will add y on both sides in the above equation, we get
$\Rightarrow 3-y+y=0+y$
As we know, the same term with opposite signs cancel out each other, thus we get
$\Rightarrow 3=y$
Therefore, the coordinates for the equation $3x-y=0$ are $\left( 0,0 \right),\left( 1,3 \right)$ ---- (5)
Similarly, we will solve equation (3), by letting different values of y and solve for x, that is
Let us suppose $y=0$ . Now, we will put it in equation (3), we get
$\Rightarrow x-0=2$
On further solving, we get
$\Rightarrow x=2$
Let us suppose $y=1$ . Now, we will put it in equation (3), we get
$\Rightarrow x-1=2$
Now, we will add 1 on both sides in the above equation, we get
$\Rightarrow x-1+1=2+1$
As we know, the same term with opposite signs cancel out each other, thus we get
$\Rightarrow x=3$
Therefore, the coordinates for the equation $x-y=2$ are $\left( 2,0 \right),\left( 3,1 \right)$ ----- (6)
Now, we will plot the value of equations (4), (5), and (6) on the graph, we get

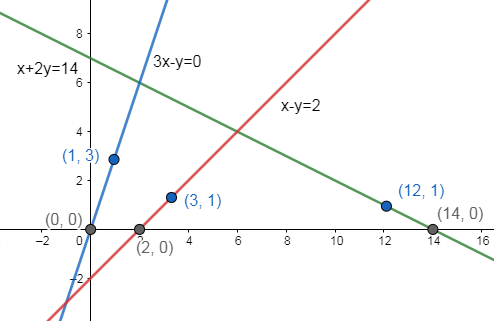
Now, we will find the shaded region for all the inequalities that is we will put the value of the variables equal to some constants, and thus find whether the inequality condition is true or false, that is
Let us suppose $\left( x,y \right)=\left( 0,0 \right)$ in equation $x+2y\le 14$ , we get
$\Rightarrow 0+2\left( 0 \right)\le 14$
Therefore, we get
$\Rightarrow 0\le 14$
It is a true statement; therefore we will shade the region for inequation $x+2y\le 14$ towards the coordinates $\left( 0,0 \right)$ -------- (7)
Let us suppose $\left( x,y \right)=\left( 1,1 \right)$ in equation $3x-y\ge 0$ , we get
$\Rightarrow 3\left( 1 \right)-1\ge 0$
Therefore, we get
$\Rightarrow 2\ge 0$
It is a true statement; therefore we will shade the region for inequation $3x-y\ge 0$ towards the coordinates $\left( 1,1 \right)$ -------- (8)
Let us suppose $\left( x,y \right)=\left( 0,0 \right)$ in equation $x-y\le 2$ , we get
$\Rightarrow 0-0\le 2$
Therefore, we get
$\Rightarrow 0\le 2$
It is a true statement, therefore we will shade the region for inequation $x-y\le 2$ towards the coordinates $\left( 0,0 \right)$ -------- (9)
So, now we will shade the values of equation (7), (8), and (9), we get

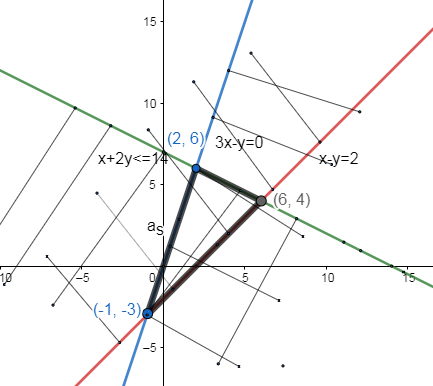
So, the end points of the closed region that is the feasibility region are $\left( 2,6 \right),\left( 6,4 \right),\left( -1,-3 \right)$ . Thus, we will not substitute the above coordinates in the objective function, which is $z=5x+3y$ , that is
We will first substitute the value $\left( 2,6 \right)$ in the objective equation, we get
$\Rightarrow z=5\left( 2 \right)+3\left( 6 \right)$
$\Rightarrow z=10+18$
Therefore, we get
$\Rightarrow z=28$ ------ (10)
We will first substitute the value $\left( 6,4 \right)$ in the objective equation, we get
$\Rightarrow z=5\left( 6 \right)+3\left( 4 \right)$
$\Rightarrow z=30+12$
Therefore, we get
$\Rightarrow z=42$ ------- (11)
We will first substitute the value $\left( -1,-3 \right)$ in the objective equation, we get
$\Rightarrow z=5\left( -1 \right)+3\left( -3 \right)$
$\Rightarrow z=-5-9$
Therefore, we get
$\Rightarrow z=-14$ ------- (12)
Thus, from the value of equation (10), (11), and (12), we get the maximal value of the linear programming as 42 and minimal value as -14.
Thus, 42 is the maximal value with the coordinate $\left( 6,4 \right)$ and -14 is the minimal value with the coordinate $\left( -1,-3 \right)$ .

Note: While solving this problem, do mention all the steps properly to avoid confusion and mathematical error. Always remember that in linear programming problems, we have to put the end points of the feasibility region in the objective function, to get the accurate answer.