Solveeit Logo
Login

Question

Question: How do you determine whether the lines for each pair of equations \(3x+2y=-5,y=-2/3x+6\) are paralle...

How do you determine whether the lines for each pair of equations 3x+2y=−5,y=−2/3x+63x+2y=-5,y=-2/3x+6 are parallel, perpendicular, or neither?

Explanation

Solution

Here in this question we have been asked to verify whether the given pair of line equations 3x+2y=−5,y=−2/3x+63x+2y=-5,y=-2/3x+6 is parallel, perpendicular or neither. For that we will find the slopes of the equations because if they are equal then the lines are parallel. If their product is equal to −1-1 then they are perpendicular.

Complete step-by-step solution:
Now considering from the question we have been asked to verify whether the given pair of line equations 3x+2y=−5,y=−2/3x+63x+2y=-5,y=-2/3x+6 is parallel, perpendicular or neither.
For doing that we will find the slopes of the equations
From the basic concepts we know that if slopes are equal then the lines are parallel. If there product is equal to −1-1 then they are perpendicular.
The slope of an equation in the form of y=mx+cy=mx+c is mm .
Hence the slope of y=−2/3x+6y=-2/3x+6 is −23\dfrac{-2}{3} .
The slope of an equation in the form of ax+by+c=0ax+by+c=0 is given as −ab\dfrac{-a}{b} .
Hence the slope of the equation 3x+2y=−5⇒3x+2y+5=03x+2y=-5\Rightarrow 3x+2y+5=0 is −32\dfrac{-3}{2} .
If we observe the slopes they are not equal, then the given pair of lines are not parallel.
The product of the slopes is given as −23×−32=1\dfrac{-2}{3}\times \dfrac{-3}{2}=1 . Therefore the lines are not perpendicular.
Hence we can conclude that the given pair of lines is neither parallel nor perpendicular.

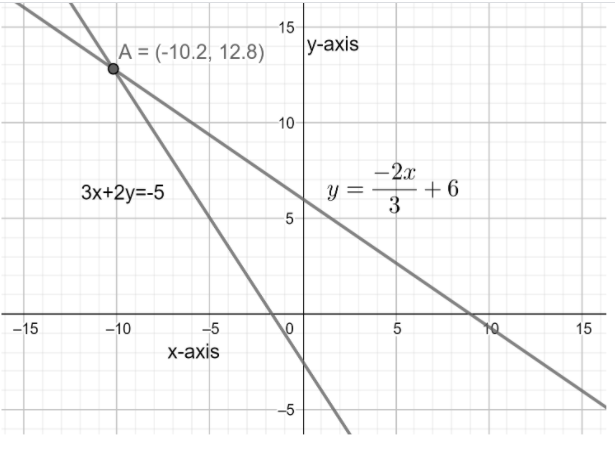
Note: While answering questions of this type we should be sure with our concept and calculations because they result in an accurate answer. The given pair of lines intersecting the intersecting point can be derived by substituting y=−2/3x+6y=-2/3x+6 in 3x+2y=−53x+2y=-5 . By doing that we will have
⇒3x+2(−2/3x+6)=−5 ⇒3x−43x+12=−5 ⇒9x−4x3=−5−12 ⇒5x3=−17 ⇒x=−10.2 \begin{aligned} & \Rightarrow 3x+2\left( -2/3x+6 \right)=-5 \\\ & \Rightarrow 3x-\dfrac{4}{3}x+12=-5 \\\ & \Rightarrow \dfrac{9x-4x}{3}=-5-12 \\\ & \Rightarrow \dfrac{5x}{3}=-17 \\\ & \Rightarrow x=-10.2 \\\ \end{aligned}.
By substituting the value of xx in any one equation we will have the value of yy as y=−2/3(−10.2)+6 ⇒y=12.8 \begin{aligned} & y=-2/3\left( -10.2 \right)+6 \\\ & \Rightarrow y=12.8 \\\ \end{aligned} .
The graph of the following pair of lines is shown below: