Solveeit Logo
Login

Question

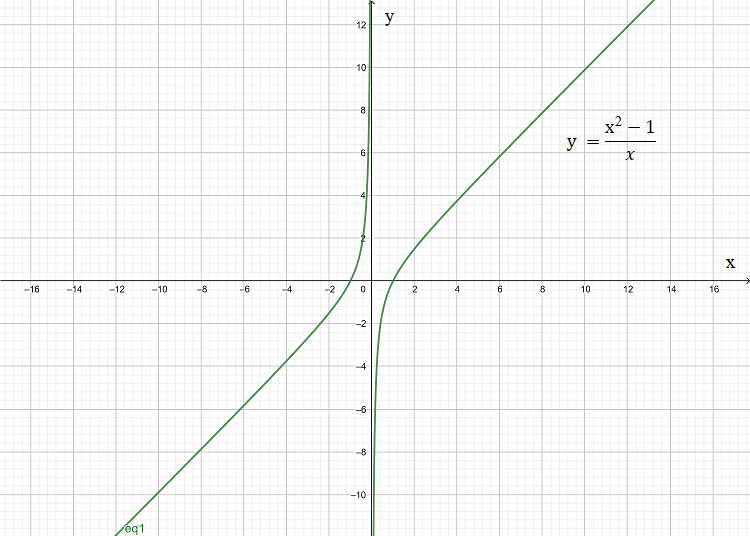
Question: How do you determine whether the graph of g(x) = \[\dfrac{{{(x)}^{2}}-1}{x}\] is symmetric with resp...

How do you determine whether the graph of g(x) = (x)2−1x\dfrac{{{(x)}^{2}}-1}{x} is symmetric with respect to the origin.

Explanation

Solution

To find whether the graph is symmetric or not it is required for us to prove that it is an odd function because an odd function will always be symmetric to origin or vice versa that is if a function is symmetric to origin then it is said to be an odd function. Here the given function is to be proved as an odd function initially as for any odd function g( −x ) = − g(x). This condition should be satisfied.

Complete step-by-step solution:
In the problem it is given that g(x) = (x)2−1x\dfrac{{{(x)}^{2}}-1}{x}
The graph of g(x) is symmetric with respect to the origin if
g( −x ) = − g(x)
That’s if g(x) is an odd function, then it is:
⇒\Rightarrow g( −x ) = (−x)2−1−x\dfrac{{{(-x)}^{2}}-1}{-x} = x2−1−x\dfrac{{{x}^{2}}-1}{-x} = −(x2−1)x-\dfrac{({{x}^{2}}-1)}{x} = − g(x)
From this we can see that g( −x ) = − g(x). so the function can be said as Odd function
So, the given function is symmetric about the origin.

Note: we should be always careful in changing the x to –x in this kind of problems as there is a possibility that we can go wrong in considering –x in the function and simplifying it. The main step in this problem is to prove the function as odd by proving g( −x ) = − g(x).