Question

How do you determine whether the function $f\left( x \right)={{x}^{4}}$ has an inverse and if it does, how do you find the inverse of this function?

Answer 1

To find whether any function has an inverse or not, we are going to test by applying the horizontal line test. In this test, we are going to draw a horizontal line on the graph and if that line cuts the curve in more than 1 point then the inverse of the function is not possible while if the horizontal line cuts the function in exactly one point then the inverse of the function exists. After checking the inverse possibility, we are going to check the inverse of a function by replacing $f\left( x \right)$ by y and then will rearrange the equation in such a way that we can write x in terms of y.

Complete step by step answer:
The function given in the above problem which we have to determine inverse of is as follows:
$f\left( x \right)={{x}^{4}}$
The graph of the above function is as follows:

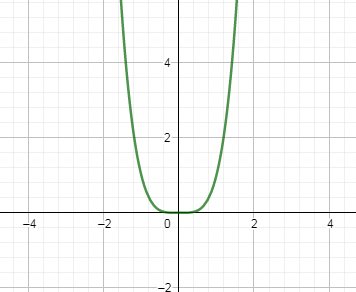
Now, let us check if the inverse of the given function is possible or not by applying a horizontal line test on the graph of the function.
Let us draw a horizontal line parallel to the x axis in the above curve.

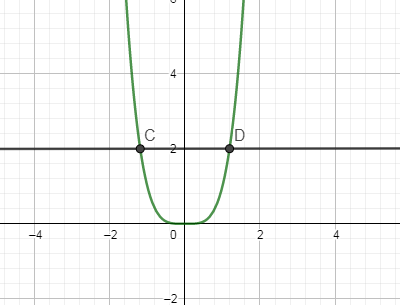
As you can see that the horizontal line cuts the curve in two points C and D so the inverse of the above function is not possible.
Now, the inverse of the given function is not possible so there is no need to determine the inverse of the given function.

Note: Generally, in exams, we have this tendency to do the calculations and try to simplify so due to this tendency, we will start finding the inverse of the function irrespective of the fact whether the inverse of the function will exist or not. So, while finding the inverse of the function, make sure to check if the inverse of the function is possible or not and then proceed further.