Question

How do you determine the limit of $\dfrac{{\sin x}}{x}$ as $x$ approaches infinity?

Answer 1

To solve this question, we can use the Squeeze Theorem, which states that if we have some function $f(x)$ , we define new functions $h(x),g(x)$ such that $h(x) \leqslant f(x) \leqslant g(x)$ . First we are considering three triangles for defining two new functions from the given function in the second quadrant of the unit circle. Then finding the area of each triangle which will give the three functions and now from those three functions we are forming the given function $\left( {\dfrac{{\sin x}}{x}} \right)$ . Then by applying the squeeze theorem we can find the limit of the function.

Complete step-by-step solution:
In this theorem, if $h(x) \leqslant f(x) \leqslant g(x)$ for all numbers, and at some point x = a then we have $h(x) = g(x)$ , the $f(x)$ must also be equal to $1.$ . In addition, we can use this theorem to find limits for $\dfrac{{\sin x}}{x}$ at x = 0, by squeezing $\dfrac{{\sin x}}{x}$ by two nicer functions and using them to find the limit at x = 0. F or a real number ‘$a$ ’ if $\mathop {\lim }\limits_{x \to a} h(x) = \mathop {\lim }\limits_{x \to a} g(x) = 1$ , then $\mathop {\lim }\limits_{x \to a} f(x)$ must be equal to $1$ .

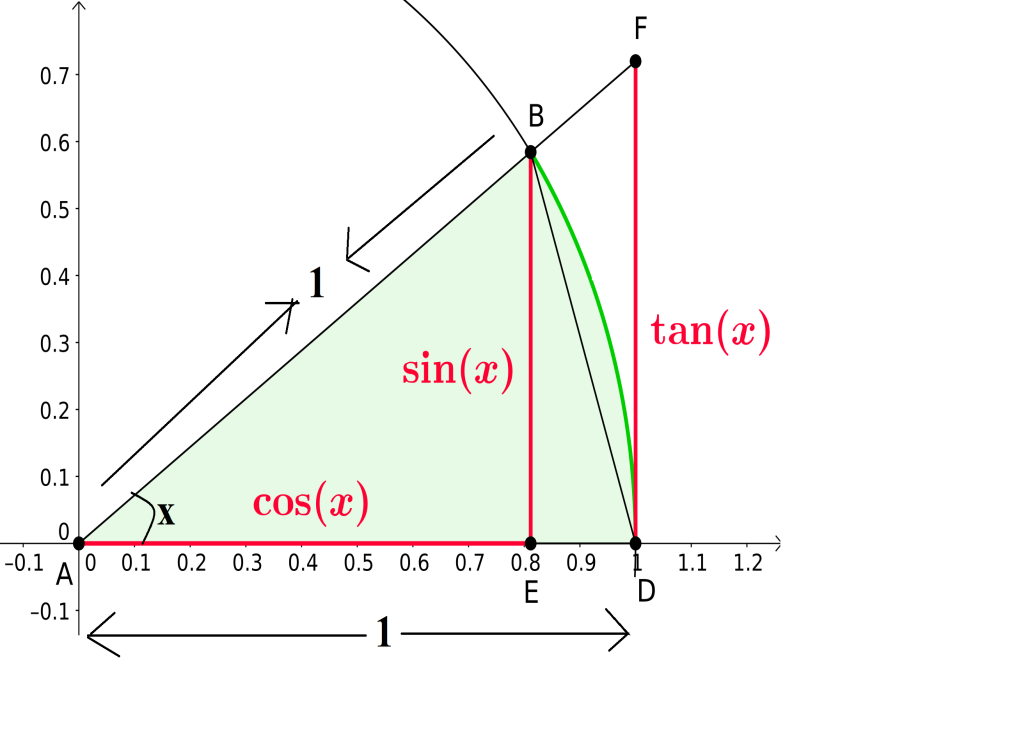
Let us Consider three triangles $\Delta ABE,\Delta ABD,\Delta AFD$
Where the Area of $\Delta ABE$ $\leqslant$ Area of $\Delta ABD$ $\leqslant$ Area of $\Delta AFD$
Area of $\Delta ABE = \dfrac{1}{2}\cos (x)\sin (x)...........(1)$
Considering $\Delta ABD$ , it is the fraction of whole circle therfore it is $\dfrac{x}{{2\pi }}$ and the whole circle has an area of $x$
$\therefore$ Area of $\Delta ABD = \dfrac{x}{{2\pi }}.\pi = \dfrac{x}{2}............(2)$
Next, the area of $\Delta AFD$ which has the base of $1$ and height of $\tan x$
$\therefore$ Area of $\Delta AFD$ $= \dfrac{1}{2}.1.\tan x$
Area of $\Delta AFD$ $= \dfrac{1}{2}.\dfrac{{\sin x}}{{\cos x}}............(3)$
Because of $\Delta ABD$ sits inside the $\Delta AFD$ and $\Delta ABE$ sits inside $\Delta ABD$
We can write
$\Rightarrow \dfrac{1}{2}\cos x.\sin x \leqslant \dfrac{x}{2} \leqslant \dfrac{1}{2}\dfrac{{\sin x}}{{\cos x}}..........(4)$
Now we are going to divide (4) equation by $\sin x$ and multiply by $2$
$\Rightarrow \cos x \leqslant \dfrac{x}{{\sin x}} \leqslant \dfrac{1}{{\cos x}}.................(5)$
To get $\dfrac{{\sin x}}{x}$ , we are going to take reciprocal of all three
$\therefore \dfrac{1}{{\cos x}} \geqslant \dfrac{{\sin x}}{x} \geqslant \cos x$
Now rearranging ,
$\Rightarrow \cos x \leqslant \dfrac{x}{{\sin x}} \leqslant \dfrac{1}{{\cos x}}...........\left( 6 \right)$
Now applying the squeeze theorem on the above equation
$h(x) \leqslant f(x) \leqslant g(x)$
We can get the values of
$\Rightarrow h(x) = \cos x$
$\Rightarrow f(x) = \dfrac{x}{{\sin x}}$
$\Rightarrow g(x) = \dfrac{1}{{\cos x}}$
Now, when $x$ approaches $0$
$\Rightarrow \mathop {\lim }\limits_{x \to 0} \cos x = 1 = \mathop {\lim }\limits_{x \to 0} \dfrac{1}{{\cos x}}$ Because $\cos \left( 0 \right) = 1$ and $\left( {\dfrac{1}{{\cos \left( 0 \right)}}} \right) = 1$
Therefore , the new defined two function is equal to $1$ and so according to the squeeze theorem the given function
$\therefore f(x) = \dfrac{x}{{\sin x}} = 1$
$\therefore \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1$

Therefore the value of $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x}$ is equal to 1.

Note: According to the diagram, we have only found the limits for $x$ approaching $0$ from the positive side but what is the limit of $x$ when it approaches $0$ from the negative side?
Now Equation $(5)$ can be written for negative side of $x$ as follows
$\Rightarrow \cos ( - x) \leqslant \dfrac{{\sin ( - x)}}{{ - x}} \leqslant \dfrac{1}{{\cos ( - x)}}$
If $x < 0$ then
$\sin ( - x) = - \sin (x)$
$\sin x = - \sin ( - x)$
If $\left( x \right)$ is negative , $\left( { - x} \right)$ is positive
$\therefore \cos x \leqslant \dfrac{x}{{\sin x}} \leqslant \dfrac{1}{{\cos x}}$ [This is the squeeze theorem we used for the positive value of $x$ ]
$\therefore$ Squeeze theorem works on both sides, therefore
$\Rightarrow \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1$
Hence the limit for the function $\left( {\dfrac{{\sin x}}{x}} \right)$ on both sides is equal to $\left( 1 \right)$