Question

How do you determine the domain, range and horizontal asymptote of each exponential function $f(x) = 1 - {2^{\left( { - \dfrac{x}{3}} \right)}}$ ?

Answer 1

In this question, we need to find the domain, range and horizontal asymptote of a given function. So first we need to know the definitions of domain, range and asymptote of a function. Domain of a function refers to the set of possible values of x for which the function will be defined and the range refers to the possible values that the function can attain for those values of x which are in the domain of $f(x)$. An asymptote is a line that the graph of a function approaches, but never touching. So the above problem is purely based on understanding the definitions related to the function and then finding each of them. Then we plot a graph to understand this clearly.

Complete step by step solution:
Given a function of the form $f(x) = 1 - {2^{\left( { - \dfrac{x}{3}} \right)}}$ …… (1)
We are asked to determine the domain, range and horizontal asymptote of the above exponential function given in the equation (1).
We need to find the domain and range of $f(x)$ using the definitions of domain and range of a function which is mentioned in the hint already.
Firstly, to find the domain we need to find the all possible values of x for which the function is defined. So, to do this we have to look at where the function goes undefined.
Note that in the given problem, there is no restriction for the variable x of the exponential function.
Hence, we can say that the domain of the given exponential function is a set of all real numbers.
i.e. the domain of $f(x) = 1 - {2^{\left( { - \dfrac{x}{3}} \right)}}$ is \left\\{ {x \in \mathbb{R}} \right\\}.
Now we find the range of the function.
We find the range for positive values of x.
Then the equation (1) can also be written as,
$f(x) = 1 - \dfrac{1}{{{2^{\dfrac{x}{3}}}}}$
Let us make x tending to infinity, i.e. as $x \to \infty$ we have,
$1 - \dfrac{1}{{{2^{\dfrac{x}{3}}}}} \to 1$, since $\dfrac{1}{{{2^{\dfrac{x}{3}}}}} \to 0$
We find the range for negative values of x.
Then the equation (1) can also be written as,
$f(x) = 1 - {2^{\dfrac{x}{3}}}$
Let us make x tending to minus infinity, i.e. as $x \to - \infty$ we have,
$1 - {2^{\dfrac{x}{3}}} \to - \infty$
So the range of the exponential function $f(x) = 1 - {2^{\left( { - \dfrac{x}{3}} \right)}}$ is \left\\{ {y \in \mathbb{R}: - \infty < y < 1} \right\\}
A horizontal asymptote for a function is a horizontal line that the graph of the function approaches as x approaches infinity or minus infinity.
The function $f(x) = a{b^x} + c$ always has a horizontal asymptote at $y = c$.
The given function can be written as, $f(x) = - {2^{ - \dfrac{x}{3}}} + 1$
Hence comparing we get $c = 1$.
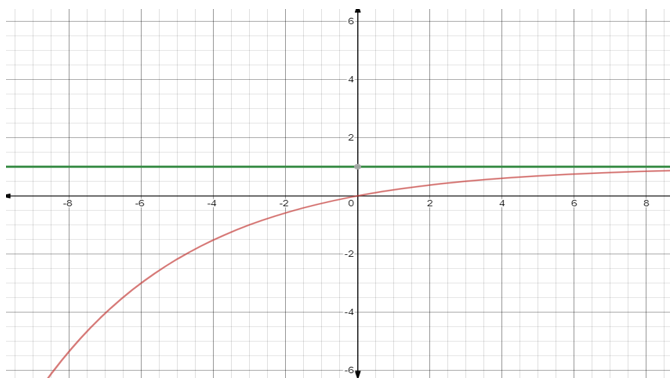
Thus, the given function $f(x) = 1 - {2^{\left( { - \dfrac{x}{3}} \right)}}$ has horizontal asymptote at $y = 1$.
Hence for a given function $f(x) = 1 - {2^{\left( { - \dfrac{x}{3}} \right)}}$ the domain is \left\\{ {x \in \mathbb{R}} \right\\}, range is \left\\{ {y \in \mathbb{R}: - \infty < y < 1} \right\\} and horizontal asymptote is at $y = 1$.
The graph of $f(x) = 1 - {2^{\left( { - \dfrac{x}{3}} \right)}}$ is given below.

Note :

1. We must know the definitions of domain, range and asymptote of the function to solve such problems.
2. Domain of a function refers to the set of possible values of x for which the function will be defined and the range refers to the possible values that the function can attain for those values of x which are in the domain of $f(x)$.
3. An asymptote is a line that the graph of a function approaches, but never touches.
4. A horizontal asymptote for a function is a horizontal line that the graph of the function approaches as x approaches infinity or minus infinity
5. The above problem can also be solved by the method of graphing, where we draw the graph and we find the values of domain and range from the values of x-axis and y-axis. And the horizontal asymptote can be observed clearly.