Solveeit Logo
Login

Question

Question: How do you determine the area to the left of \(g\left( y \right)=3-{{y}^{2}}\) and to the right of \...

How do you determine the area to the left of g(y)=3−y2g\left( y \right)=3-{{y}^{2}} and to the right of x=−1x=-1 ?

Explanation

Solution

We have been given two functions and we have to find the area enclosed by those functions. The left boundary of the area enclosed is x=−1x=-1 and the area is contained by the function g(y)=3−y2g\left( y \right)=3-{{y}^{2}}. We shall first plot these two functions on the same cartesian plane and find their two points of intersections. Then we shall perform definite integration on the function g(y)=3−y2g\left( y \right)=3-{{y}^{2}} taking the two points of intersections as the limits.

Complete step-by-step solution:
Given are two functions g(y)=3−y2g\left( y \right)=3-{{y}^{2}} and x=−1x=-1 where one function is straight-line parallel to the y-axis and the other function is parabolic in nature.

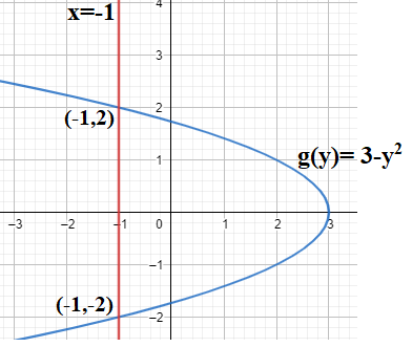
Here, we see that the points of intersection of these two functions are (−1,2)\left( -1,2 \right) and (−1,−2)\left( -1,-2 \right).
Thus, the required region is the shaded region in the graph below.

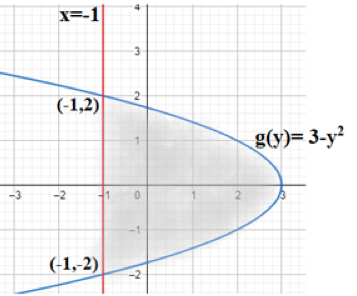
In order to find the enclosed area, we shall integrate g(y)=3−y2g\left( y \right)=3-{{y}^{2}} from y=2y=2 to y=−2y=-2.
A=∫−223−y2.dyA=\int\limits_{-2}^{2}{3-{{y}^{2}}.dy}
From the basic properties of integration, we know that ∫3.dy=3y+C\int{3.dy=3y}+C and ∫yn.dy=yn+1n+1+C\int{{{y}^{n}}.dy=\dfrac{{{y}^{n+1}}}{n+1}}+C. We shall use these properties to integrate our function.
⇒A=3y−y33∣−22\Rightarrow A=\left. 3y-\dfrac{{{y}^{3}}}{3} \right|_{-2}^{2}
Now, we will apply the upper limit of the integral equal to 2 and the lower limit of the integral equal to -2.
⇒A=3(2)−(2)33−(3(−2)−(−2)33)\Rightarrow A=3\left( 2 \right)-\dfrac{{{\left( 2 \right)}^{3}}}{3}-\left( 3\left( -2 \right)-\dfrac{{{\left( -2 \right)}^{3}}}{3} \right)
Since 23=2×2×2=8{{2}^{3}}=2\times 2\times 2=8, thus substituting 23=8{{2}^{3}}=8, we get
⇒A=6−83−(−6−(−8)3)\Rightarrow A=6-\dfrac{8}{3}-\left( -6-\dfrac{\left( -8 \right)}{3} \right)
⇒A=6−83+6−83\Rightarrow A=6-\dfrac{8}{3}+6-\dfrac{8}{3}
⇒A=12−163\Rightarrow A=12-\dfrac{16}{3}
⇒A=203\Rightarrow A=\dfrac{20}{3}
Therefore, the area to the left of g(y)=3−y2g\left( y \right)=3-{{y}^{2}} and to the right of x=−1x=-1 is 203\dfrac{20}{3} square units.

Note: Definite integral of a function f(y)f\left( y \right) is the area bound under the graph of function, x=f(y)x=f\left( y \right)and above the y-axis which is bound between two bounds as y=ay=a and y=by=b. Here, a=a= -2 and b=b=2. The best thing about integral calculus is that the one of the two boundaries of the area to be found is a curve and the other boundary is the y-axis when the function is being integrated with respect to dydy.