Question

How do you determine the amplitude of $y=\cos x$ ?

Answer 1

We have been given a trigonometric function namely the cosine function. The coefficient of this function is equal to 1. We know that the amplitude of a function is defined as how far the function varies from its mid-line either how far above it goes or how far below it goes. Thus, we shall determine its amplitude by sketching the graph of the cosine function.

Complete step by step answer:
The mid-line of a function is a horizontal line on the graph of the function where half of the function is above it and half of the function is below it whereas the amplitude of a periodic function is just half the difference between the minimum and maximum values it taken on.
The graph of $y=\cos x$ is given as:

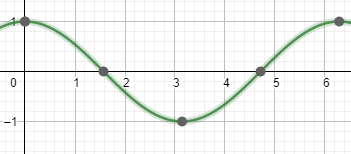
The mid-line of cosine function is the x-axis itself. Thus, we can see that the maximum value $\left( \max \right)$ of the graph is equal to 1 and the minimum value $\left( \min \right)$ of the graph is equal to -1.
$amplitude=\dfrac{\max -\min }{2}$
$\Rightarrow amplitude=\dfrac{1-\left( -1 \right)}{2}$
$\Rightarrow amplitude=\dfrac{2}{2}$
$\Rightarrow amplitude=1$

Therefore, the amplitude of $y=\cos x$ is equal to 1.

Note: Another way of thinking about the amplitude of a periodic function is the amount by which it sways from its middle position. A function is said to be periodic in nature when it starts repeating itself after a fixed interval on the x-axis. This fixed interval on the x-axis is known as the period of the function which changes when there is a change in the coefficient of the input value $\left( x \right)$ of the function. Here, the coefficient of the input value is 1, thus the period of cosine function does not change.