Question

How do you determine if $x\sin x$ is an even or odd function?

Answer 1

In mathematics, a function is defined as a binary relation between two sets that relates each element of the first set to exactly one set in the second set. Suppose that ‘A’ and ‘B’ are two sets. Then a function relating these two sets is written as $f:A \to B$. Read as $'f{\text{ maps }}A{\text{ to }}B'$.
Odd functions and even functions are functions which satisfy a particular symmetric relation.
Even function:
Let $f$ be a real-valued function. Then, $f$ is said to be an even function if $f(x) = f( - x)$
For example, take a function $f(x) = \cos x$
So, substitute $- x$ in place of $x$.
$\Rightarrow f( - x) = \cos ( - x)$
And we know that, $\cos ( - x) = \cos x$
$\Rightarrow f( - x) = \cos ( - x) = \cos x$
When we observe here, $f(x)$ and $f( - x)$ are equal. So, $f( - x) = f(x)$
So, $f$ is an even function.
Odd function:
Let $f$ be a real-valued function. Then, $f$ is said to be an odd function if $f( - x) = - f(x)$
For example, take a function $f(x) = {x^3}$
So, substitute $- x$ in place of $x$.
$\Rightarrow f( - x) = {\left( { - x} \right)^3}$
$\Rightarrow f( - x) = {\left( { - 1 \times x} \right)^3} = - {x^3}$
When we observe this, $f(x)$ and $f( - x)$ are additive inverse to each other. So, $f( - x) = - f(x)$.
So, $f$ is an odd function.

Complete step by step solution:
Now, the given question is $x\sin x$
So, take $f(x) = x\sin x$
So, substitute $- x$ in place of $x$.
$\Rightarrow f( - x) = ( - x)(\sin ( - x))$
$\Rightarrow f( - x) = ( - x)( - \sin x)$
So, we get the final result as,
$\Rightarrow f( - x) = x\sin x$
When we observe here, $f(x)$ and $f( - x)$ are equal. So, $f( - x) = f(x)$
Therefore, $x\sin x$ is an even function.
We can see the graph of $x \sin x$ below

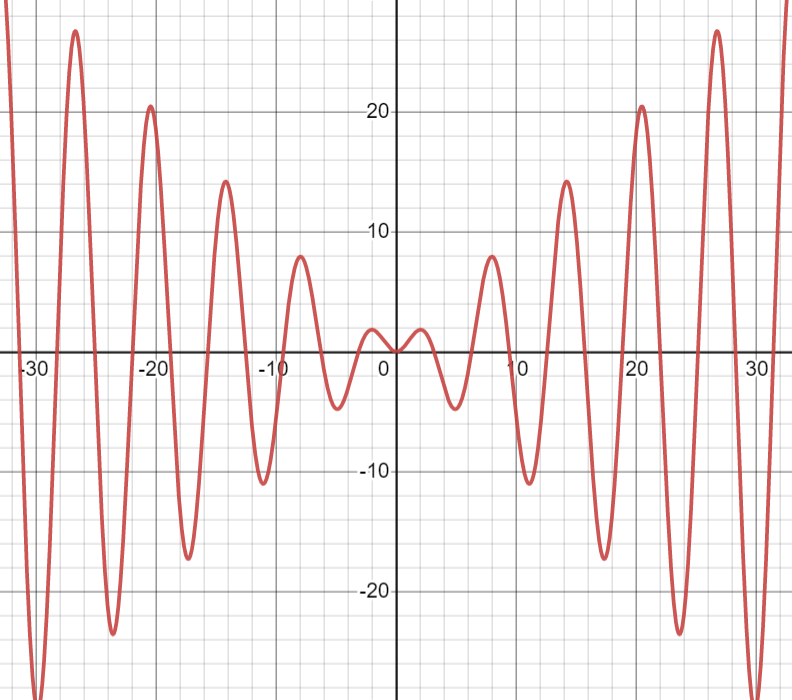
Note:
If you plot graphs for functions like $y = f(x)$, then an even function is symmetrical about the Y-axis. And an odd function is not symmetrical about the Y-axis.
Another form of defining an even function is, if $f(x) - f( - x) = 0$, then $f(x)$ is an even function.
And similarly, if $f( - x) + f(x) = 0$, then $f(x)$ is an odd function.