Solveeit Logo
Login

Question

Question: How do you determine circle, parabola, ellipse or hyperbola from the equation \({{x}^{2}}+{{y}^{2}}-...

How do you determine circle, parabola, ellipse or hyperbola from the equation x2+y2−16x+18y−11=0{{x}^{2}}+{{y}^{2}}-16x+18y-11=0?

Explanation

Solution

We will first try to group the terms present in the equation and then complete the square for both x and y terms. Then we will compare the obtained equation with the general equations of circle, parabola, ellipse and hyperbola to get the desired answer.

Complete step-by-step solution:
We have been given an equation x2+y2−16x+18y−11=0{{x}^{2}}+{{y}^{2}}-16x+18y-11=0.
We have to determine whether the given equation is of circle, parabola, ellipse or hyperbola.
Now, let us group the x and y terms then we will get
⇒x2−16x+y2+18y=11\Rightarrow {{x}^{2}}-16x+{{y}^{2}}+18y=11
Now, to complete the square for x we need to add 64 both sides of the equation. Then we will get
⇒x2−16x+64+y2+18y=11+64 ⇒x2−8×2x+82+y2+18y=11+64 ⇒(x−8)2+y2+18y=75 \begin{aligned} & \Rightarrow {{x}^{2}}-16x+64+{{y}^{2}}+18y=11+64 \\\ & \Rightarrow {{x}^{2}}-8\times 2x+{{8}^{2}}+{{y}^{2}}+18y=11+64 \\\ & \Rightarrow {{\left( x-8 \right)}^{2}}+{{y}^{2}}+18y=75 \\\ \end{aligned}
Now, to complete the square for y we need to add 81 both sides of the equation. Then we will get
⇒(x−8)2+y2+18y+81=75+81 ⇒(x−8)2+y2+2×9y+92=156 ⇒(x−8)2+(y+9)2=156 \begin{aligned} & \Rightarrow {{\left( x-8 \right)}^{2}}+{{y}^{2}}+18y+81=75+81 \\\ & \Rightarrow {{\left( x-8 \right)}^{2}}+{{y}^{2}}+2\times 9y+{{9}^{2}}=156 \\\ & \Rightarrow {{\left( x-8 \right)}^{2}}+{{\left( y+9 \right)}^{2}}=156 \\\ \end{aligned}
Now, we know that the above obtained equation is similar to the standard equation of circle which is given as (x−h)2+(y−k)2=r2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}

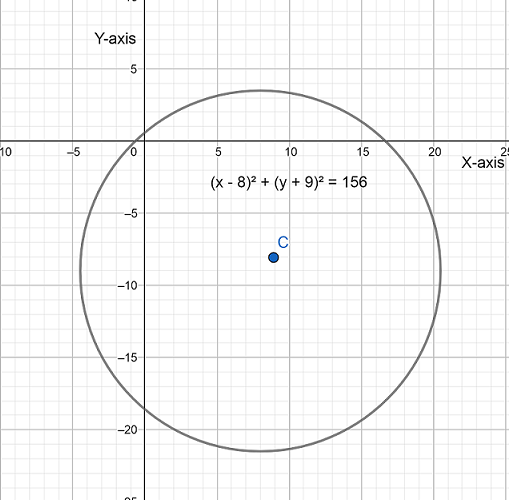
Hence the given equation represents the circle.

Note: Alternatively by analyzing some points we can determine whether the equation belongs to a circle, parabola, ellipse or hyperbola.
If the coefficients of both x2{{x}^{2}} and y2{{y}^{2}} are the same then it is a circle. If the coefficients of both x2{{x}^{2}} and y2{{y}^{2}} are different and have positive or negative value then it is an ellipse. If there is only one squared term then it is a parabola and if there is one squared term and has negative coefficient then it is a hyperbola.
From the above points the given equation has the same coefficients of both x2{{x}^{2}} and y2{{y}^{2}} so it is an equation of circle.