Question

How do you convert ${x^2} + {y^2} = 4x$ into polar form?

Answer 1

We use the substitution of ‘x’ and ‘y’ in terms of polar coordinates of ‘r’ i.e. the radius of the circle. Substitute and convert the given equation in form of ‘r’ and given angle. Use the trigonometric identity ${\cos ^2}\theta + \sin {\theta ^2} = 1$ to make the equation simpler. Cancel possible factors and write the polar from in the simplest form.

• Polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction.
  For any point $(x,y)$ in the Cartesian plane, we use the conversion formula $x = r\cos \theta ;y = r\sin \theta$ to convert in polar coordinates.
  

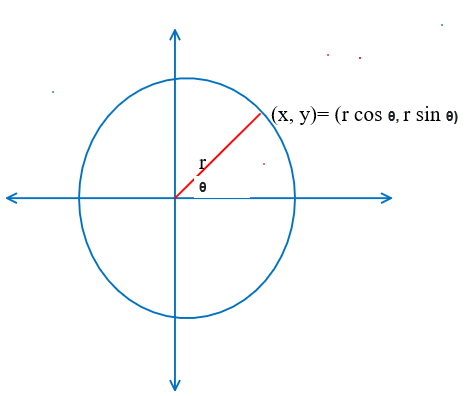
Complete step by step solution:
We are given the equation ${x^2} + {y^2} = 4x$ … (1)
Since, we have an equation with points in Cartesian plane i.e. $(x,y)$, so we can convert the equation in polar form by using substitution $x = r\cos \theta ;y = r\sin \theta$ in the equation
$\Rightarrow {(r\cos \theta )^2} + {(r\sin \theta )^2} = 4r\cos \theta$
$\Rightarrow {r^2}{\cos ^2}\theta + {r^2}\sin {\theta ^2} = 4r\cos \theta$
Take ${r^2}$common and collect two terms
$\Rightarrow {r^2}\left( {{{\cos }^2}\theta + \sin {\theta ^2}} \right) = 4r\cos \theta$
Substitute the value of ${\cos ^2}\theta + \sin {\theta ^2} = 1$
$\Rightarrow {r^2} = 4r\cos \theta$
Cancel same factor i.e. ‘r’ from both sides of the equation
$\Rightarrow r = 4\cos \theta$
Shift constant value to left side of the equation
$\Rightarrow r - 4\cos \theta = 0$
$\therefore$ Conversion of ${x^2} + {y^2} = 4x$ in polar form is $r - 4r\cos \theta = 0$.

Note: Many students think polar coordinates are $r,\theta$, so they just simply write these coordinates in place of Cartesian coordinates, keep in mind the value for conversion from Cartesian to polar coordinates is $x = r\cos \theta ;y = r\sin \theta$, so we have to use substitution and then convert. Also, many students tend to leave the answer in the form of a quadratic equation which is wrong,, keep in mind if we show the polar form is a quadratic equation then we will have to find the roots of the quadratic equation as well. It is always recommended to cancel off common factors.