Question

How do you convert $x=-1$ to slope intercept form?

Answer 1

To carry out the conversion, we at first check the slope of the given line. If the slope comes out to be infinite, we can say that the intercept will also be infinite and that the slope intercept form of the straight line becomes indeterminate and unable to express.

Complete step by step solution:
The given equation that we have at our disposal is,
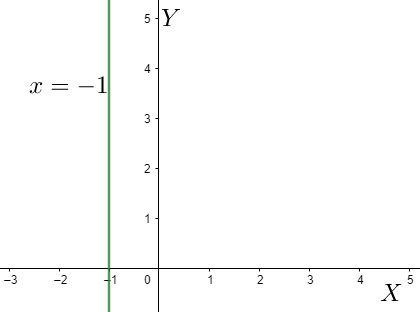
$x=-1$
Since, the above equation is a linear equation, we can say that the equation is the equation of a line. Now, there are various ways to represent the equation of a straight line. They are:
a. General form: $ax+by=c$
b. Slope intercept form: $y=mx+c$
c. Intercept form: $\dfrac{x}{a}+\dfrac{y}{b}=1$
In this problem, we have to use the slope intercept form. The slope intercept form is $y=mx+c$ . Here, $x$ is the independent variable, $y$ is the dependent variable, $m$ is the slope of the line and $c$ is the $y$ -intercept. $y$ -intercept means the length of the line segment joining the origin and the point of intersection of the line and the $y$ -axis.
If we observe the given line closely, we can see that the line has a constant value of $x$ which is equal to $-1$ . Nothing is mentioned as such about $y$ . This clearly indicates one thing. The value of $x$ is constant and from this value of $x$ alone, we cannot determine the value of $y$ . This means that the value of $x$ remaining constant, $y$ attains all possible values on the number line. This is nothing but a line parallel to the $y$ -axis. This type of line makes an angle ${{90}^{\circ }}$ with the positive $x$ -axis. So, the slope will be $\tan {{90}^{\circ }}=\infty$ and since it is parallel to the $y$ -axis, the $y$ -intercept is also $\infty$ .
Therefore, we can conclude that the given line cannot be represented in the slope intercept form as it attains the indeterminate form.

Note: Before solving these types of problems, we should make sure whether the line is parallel to the $x$ or the $y$ axes. An equation of the form $x=a$ is a line parallel to the y-axis and $y=a$ is a line parallel to the x-axis. This can also be checked by plotting the graph of the line.