Question

How do you convert the equation ${{x}^{2}}-{{y}^{2}}=1$ in polar form?

Answer 1

We start solving the problem by assuming the point on the curve representing the given equation. We then assume variables for the distance between the origin and that point, and the angle made by the line joining the origin and that point to proceed through the problem. We then find the relation of x and y in terms of the assumed distance and angle. We then substitute the obtained relations in the given equation. We then make the necessary calculations to get the relation between the distance and angle which will give us the required answer.

Complete step by step answer:
According to the problem, we are asked to convert the given equation ${{x}^{2}}-{{y}^{2}}=1$ into the polar form.
We have given the equation ${{x}^{2}}-{{y}^{2}}=1$ ---(1).
Let us assume $\left( x,y \right)$ be the point on the given curve. We need to convert this point to $\left( r,\theta \right)$, where r is the distance between the origin and the point $\left( x,y \right)$ and $\theta$ is the angle made by the line joining the origin and the point $\left( x,y \right)$ with x-axis. Let us draw a figure representing this information.

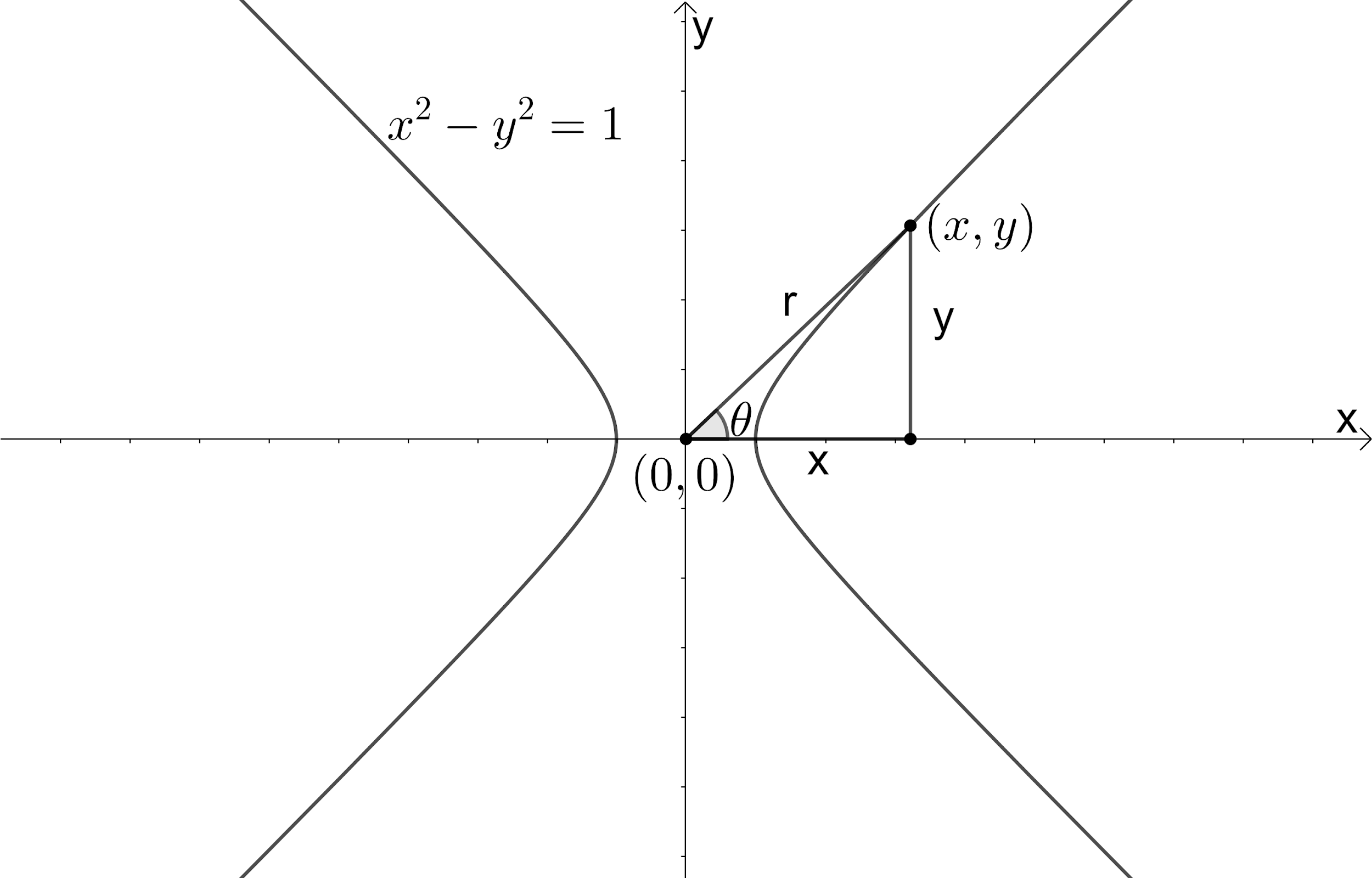
We know that in a right-angle triangle cosine of any angle is the ratio of the adjacent side to the hypotenuse and sine of any angle is the ratio of the opposite side to the hypotenuse.
From the figure, we can see that $\cos \theta =\dfrac{x}{r}\Leftrightarrow x=r\cos \theta$ and $\sin \theta =\dfrac{y}{r}\Leftrightarrow y=r\sin \theta$ ---(2).
Let us substitute equation (2) in equation (1).
$\Rightarrow {{\left( r\cos \theta \right)}^{2}}-{{\left( r\sin \theta \right)}^{2}}=1$.
$\Rightarrow {{r}^{2}}{{\cos }^{2}}\theta -{{r}^{2}}{{\sin }^{2}}\theta =1$.
$\Rightarrow {{r}^{2}}\left( {{\cos }^{2}}\theta -{{\sin }^{2}}\theta \right)=1$.
We know that $\cos 2\theta ={{\cos }^{2}}\theta -{{\sin }^{2}}\theta$.
$\Rightarrow {{r}^{2}}\cos 2\theta =1$.
We know that ${{r}^{2}}>0$, as r is the distance. This tells us that $\cos 2\theta >0$.
$\Rightarrow {{r}^{2}}=\dfrac{1}{\cos 2\theta }$.
$\Rightarrow r=\dfrac{1}{\sqrt{\cos 2\theta }}$.
So, we have found the polar form of ${{x}^{2}}-{{y}^{2}}=1$ as $\left( \dfrac{1}{\sqrt{\cos 2\theta }},\theta \right)$.
$\therefore$ The polar form of ${{x}^{2}}-{{y}^{2}}=1$ is $\left( \dfrac{1}{\sqrt{\cos 2\theta }},\theta \right)$.

Note:
We should perform each step carefully in order to avoid calculation mistakes and confusion. We should keep in mind that the polar form of every point present on the curve can be formed using the obtained form while solving this problem. Whenever we get this type of problem, we first try to assume variables for unknowns to make the process simpler. Similarly, we can expect problems to find the polar form of the equation ${{x}^{2}}+{{y}^{2}}=16$.