Question

How do you convert $r=\sin 2\theta$ in rectangular form?

Answer 1

We have to convert the given equation $r=\sin 2\theta$ into rectangular form. Rectangular form means we have to convert $\theta$ in terms of x and y. We are also going to use the trigonometric identity i.e. $\sin 2\theta =2\sin \theta \cos \theta$. The “r” in this equation is the magnitude of the vector and that vector is making an angle $\theta$ with the x axis. The x component of this vector is equal to $r\cos \theta$ so we are going to use this relation in the conversion.

Complete answer:
In the above problem, we are asked to convert the following into rectangular form:
$r=\sin 2\theta$
We know the trigonometric identity that:
$\sin 2\theta =2\sin \theta \cos \theta$
So, we are going to use the above trigonometry relation in $r=\sin 2\theta$ we get,
$r=2\sin \theta \cos \theta$
Now, the rectangular form means the x and y Cartesian coordinates so we are going to draw a vector “r” which is making angle $\theta$ with the x axis.

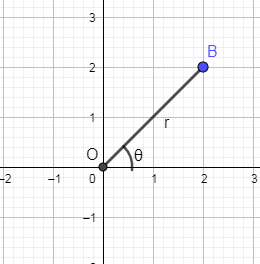
Now, we are going to show the x projection of the vector r in the above graph.

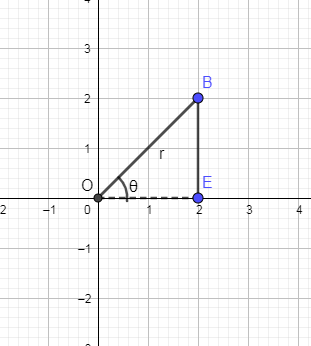
OE is the x projection of the vector “r”. We know from the vector projection that:
$r\cos \theta =OE$
And as OE is the x component of the vector “r” so we can write OE as x in the above and we get,
$r\cos \theta =x$
Now, dividing “r” on both the sides we get,
$\cos \theta =\dfrac{x}{r}$
We know there is trigonometric identity that:
${{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta$
Taking square root on both the sides of the above equation we get,
$\begin{aligned} & \sqrt{{{\sin }^{2}}\theta }=\sqrt{1-{{\cos }^{2}}\theta } \\\ & \Rightarrow \sin \theta =\sqrt{1-{{\cos }^{2}}\theta } \\\ \end{aligned}$
Now, substituting the value of $\cos \theta$ from $\cos \theta =\dfrac{x}{r}$ we get,

& \sin \theta =\sqrt{1-{{\left( \dfrac{x}{r} \right)}^{2}}} \\\ & \Rightarrow \sin \theta =\sqrt{\dfrac{{{r}^{2}}-{{x}^{2}}}{{{r}^{2}}}} \\\ \end{aligned}$$ $$\Rightarrow \sin \theta =\dfrac{\sqrt{{{r}^{2}}-{{x}^{2}}}}{r}$$ Substituting the above values of $\sin \theta \And \cos \theta $ in $r=2\sin \theta \cos \theta $ we get, $\begin{aligned} & r=2\left( \dfrac{x}{r} \right)\left( \dfrac{\sqrt{{{r}^{2}}-{{x}^{2}}}}{r} \right) \\\ & \Rightarrow r=2\left( \dfrac{x}{{{r}^{2}}} \right)\left( \sqrt{{{r}^{2}}-{{x}^{2}}} \right) \\\ \end{aligned}$ And “r” is the magnitude of the vector which is equal to: $\sqrt{{{x}^{2}}+{{y}^{2}}}$ So, substituting this value of r in the above “r” equation we get, $\begin{aligned} & r=2\left( \dfrac{x}{{{r}^{2}}} \right)\left( \sqrt{{{r}^{2}}-{{x}^{2}}} \right) \\\ & \Rightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}=2\left( \dfrac{x}{{{\left( \sqrt{{{x}^{2}}+{{y}^{2}}} \right)}^{2}}} \right)\left( \sqrt{{{\left( \sqrt{{{x}^{2}}+{{y}^{2}}} \right)}^{2}}-{{x}^{2}}} \right) \\\ & \Rightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}=2\left( \dfrac{x}{{{x}^{2}}+{{y}^{2}}} \right)\sqrt{\left( {{x}^{2}}+{{y}^{2}}-{{x}^{2}} \right)} \\\ \end{aligned}$ Positive and negative ${{x}^{2}}$ will be cancelled out in square root expression written on the R.H.S of the above equation we get, $\begin{aligned} & \sqrt{{{x}^{2}}+{{y}^{2}}}=2\left( \dfrac{x}{{{x}^{2}}+{{y}^{2}}} \right)\sqrt{\left( {{y}^{2}} \right)} \\\ & \Rightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}=2\left( \dfrac{x}{{{x}^{2}}+{{y}^{2}}} \right)\left( y \right) \\\ \end{aligned}$ Multiplying $\left( {{x}^{2}}+{{y}^{2}} \right)$ on both the sides of the above equation we get, $\begin{aligned} & \sqrt{{{x}^{2}}+{{y}^{2}}}\left( {{x}^{2}}+{{y}^{2}} \right)=2xy \\\ & \Rightarrow {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{\dfrac{3}{2}}}=2xy \\\ \end{aligned}$ Hence, we have written the given equation into rectangular form as ${{\left( {{x}^{2}}+{{y}^{2}} \right)}^{\dfrac{3}{2}}}=2xy$. **Note:** To solve the above problem, you should know the relation between the vector and the angle made by the vector with x axis. This is the vector projection concept. Another thing that you can find from the above solution is the y component of the vector “r” which is equal to: $y=r\sin \theta $ And in the below, we have shown the y component of vector “r” graphically,  In the above graph, OF is the y component of the vector “r”.