Question

How do you convert $r\cos \left( \theta \right)=4$ into rectangular form?

Answer 1

A complex number in the polar form is represented in terms of the distance from the origin, $r$ and the angle made with the x-axis, $\theta$. And in the rectangular form it is represented in the form of the rectangular coordinates, x and y. Considering a complex number in the x-y plane we can determine the relation between its polar and the rectangular coordinates. On substituting the relation into the given equation $r\cos \left( \theta \right)=4$, we can write the required rectangular form.

Complete step by step answer:
In the above question, we have been given a complex number in the polar form. We know that a complex number can be represented in two forms, which are the polar form and the rectangular form. In the polar form, we represent a complex number by its two parameters; first one is its distance from the origin, $r$ and the second one is the angle made by it with the positive direction of the x axis, $\theta$. While in the rectangular form, the complex number is represented in the form of its polar coordinates; $x$ and $y$.
Consider a complex number represented by a point P in the x-y plane as shown in the figure below.

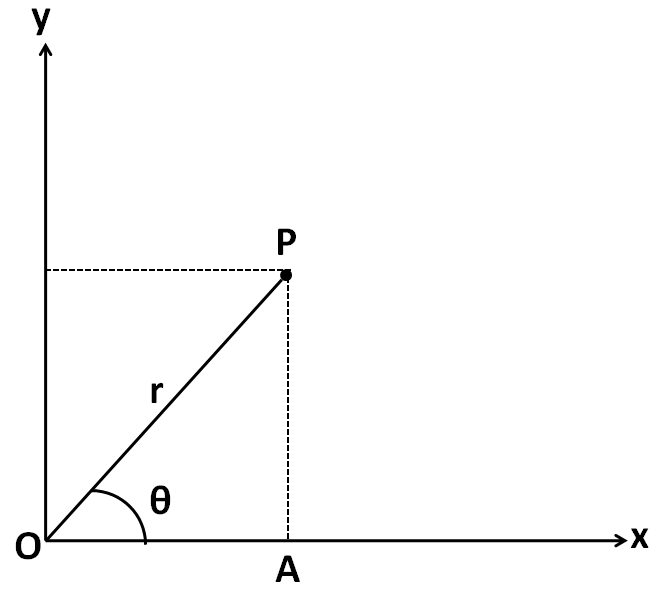
For representing it in the rectangular form, we need to determine its x and y coordinates. In the triangle OAP, we have
$\begin{aligned} & \Rightarrow \cos \theta =\dfrac{OA}{OP} \\\ & \Rightarrow \cos \theta =\dfrac{OA}{r} \\\ \end{aligned}$
Multiplying both sides by $r$ we get
$\Rightarrow OA=r\cos \theta$
From the above figure, the x-coordinate of the point P is equal to $OA$. SO we have
$\Rightarrow x=r\cos \theta .........(i)$
Similarly we have
$\begin{aligned} & \Rightarrow \sin \theta =\dfrac{PA}{OP} \\\ & \Rightarrow \sin \theta =\dfrac{PA}{r} \\\ & \Rightarrow PA=r\sin \theta \\\ & \Rightarrow y=r\sin \theta ........(ii) \\\ \end{aligned}$
Equations (i) and (ii) together are the required relations between the polar and the rectangular coordinates of the complex number.
Now, in the given question we have
$r\cos \left( \theta \right)=4$
Substituting (i) in the above equation, we get
$\begin{aligned} & \Rightarrow r\left( \dfrac{x}{r} \right)=4 \\\ & \Rightarrow x=4 \\\ \end{aligned}$
This is the required rectangular form of $r\cos \left( \theta \right)=4$.

Note: In the above question, we had no information regarding the y-coordinate of the complex number. This occurred because in the polar form we have two variables, $r$ and $\theta$. But we were given only a single equation, that is $r\cos \left( \theta \right)=4$. So we could only determine the x-coordinate of the complex number. Otherwise, in the rectangular form the complex number is written as $x+iy$.