Solveeit Logo
Login

Question

Question: How do you convert r = 3 in rectangular form?...

How do you convert r = 3 in rectangular form?

Explanation

Solution

We will first find r in terms of x and y. Then we will have a circle with centre as origin. We can draw the circle and join the x – coordinate at the line to x – axis and similarly y – axis.

Complete step by step solution:
We are given that we are required to convert r = 3 in the rectangular form.
Since, we know that in polar form, r2=x2+y2{r^2} = {x^2} + {y^2}.
Taking the square – root of the above equation on both the sides, we will then obtain the following equation:-
⇒r=x2+y2\Rightarrow r = \sqrt {{x^2} + {y^2}}
Putting this in the given equation r = 3, we will then obtain the following equation as:-
⇒x2+y2=3\Rightarrow \sqrt {{x^2} + {y^2}} = 3
Taking the square of the above equation on both the sides, we will then obtain the following equation:-
⇒x2+y2=32\Rightarrow {x^2} + {y^2} = {3^2}
Simplifying the calculations on the right hand side of the above equation, we will then obtain the following equation with us:-
⇒x2+y2=9\Rightarrow {x^2} + {y^2} = 9
Plotting this circle on the axis, we will then obtain the following equation as:-

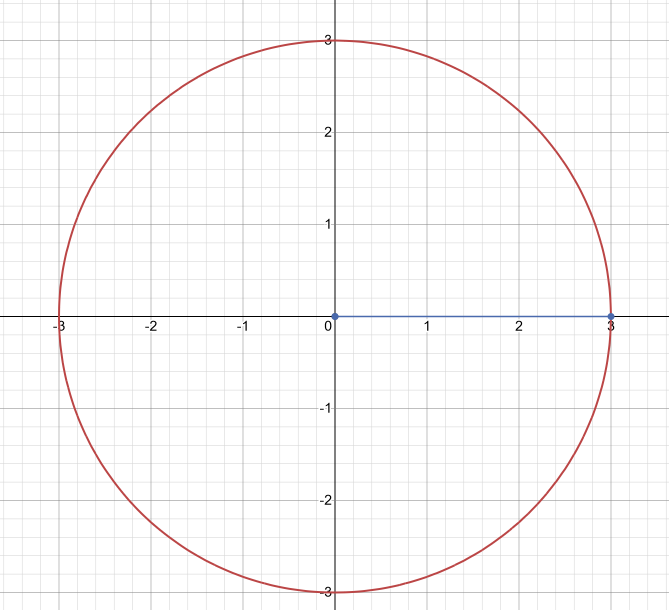
Now, if we wish to convert this in rectangular form, we will then get the following image:-

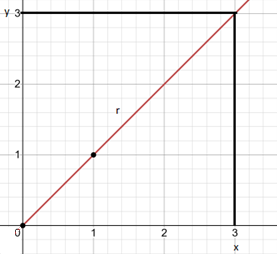
Thus, we have the required answer.

Note: The students must note that in the rectangular form, we just took the point on the circle and joined it to both the x and y – axis to get the rectangular form.
The students must know that in polar form, we assume that:
⇒x=rcos⁡θ\Rightarrow x = r\cos \theta
⇒y=rsin⁡θ\Rightarrow y = r\sin \theta
Squaring both the above equations on both the sides, we will then obtain the following equations:-
⇒x2=r2cos⁡2θ\Rightarrow {x^2} = {r^2}{\cos ^2}\theta
⇒y2=r2sin⁡2θ\Rightarrow {y^2} = {r^2}{\sin ^2}\theta
Adding both the above equations, we will then obtain the following equation as:-
⇒x2+y2=r2cos⁡2θ+r2sin⁡2θ\Rightarrow {x^2} + {y^2} = {r^2}{\cos ^2}\theta + {r^2}{\sin ^2}\theta
Taking r2{r^2} common from both the terms in the right hand side, we will then obtain the following equation as:-
⇒x2+y2=r2(cos⁡2θ+sin⁡2θ)\Rightarrow {x^2} + {y^2} = {r^2}\left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right)
Since, we know that we have an identity which states that: cos⁡2θ+sin⁡2θ=1{\cos ^2}\theta + {\sin ^2}\theta = 1. Thus, we have:-
⇒x2+y2=r2×1\Rightarrow {x^2} + {y^2} = {r^2} \times 1
Simplifying the calculations on the right hand side in the above equation, we will then obtain the following equation:-
⇒x2+y2=r2\Rightarrow {x^2} + {y^2} = {r^2}