Question

How do you convert $r = 1 + \cos (\theta )$ into rectangular form?

Answer 1

Use the equations $x = r\cos \theta$ and $y = r\sin \theta$ to find values of $\cos \theta$ and r. Square and add these two terms to get the value of r. Substitute the values of r and $\cos \theta$ to make the equation in terms of x and y.

Complete Step by Step Solution:
In order to convert the polar coordinates i.e., $\left( {r,\theta } \right)$ to rectangular coordinates, we use the following set of equations:
$\Rightarrow x=r\cos \theta$
$\Rightarrow y = r\sin \theta$
Squaring both sides and adding the equations, we get
$\Rightarrow {x^2} + {y^2} = {r^2}{\cos ^2}\theta + {r^2}{\sin ^2}\theta$
Taking ${r^2}$ common from the right-hand side of the above equation,
$\Rightarrow {x^2} + {y^2} = {r^2}({\sin ^2}\theta + {\cos ^2}\theta )$
Using the identity: ${\sin ^2}\theta + {\cos ^2}\theta = 1$ , the equation can be simplified as
$\Rightarrow {x^2} + {y^2} = {r^2}$
The value of r thus becomes, $r = \sqrt {{x^2} + {y^2}}$
From the question, we know that $r = 1 + \cos (\theta )$
Multiplying both sides of the equation by r, the equation becomes
${\Rightarrow r^2} = r + r\cos \theta$
Substituting ${r^2} = {x^2} + {y^2}$, $r = \sqrt {x + y}$ and $r\cos \theta = x$ we can rewrite the equation as

${x^2} + {y^2} = \sqrt {{x^2} + {y^2}} + x$, which is the required equation in the rectangular form.

Note:
Any point in a two-dimensional plane can be defined by an x and y coordinate. The origin is the point where the values of both x and y are zero. When we move x units right from the origin and y units up, we get a point the coordinates of which are (x, y). These are called the rectangular coordinates of a point.

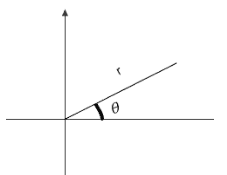
Consider a point along some radius, r. However, r isn’t enough to determine the position of a point. Another factor we consider is the angle $\theta$. The line r makes an angle, $\theta$ with the X-axis. The point is labelled as $(r,\theta )$ . These are known as the polar coordinates of the point.