Question

How do you convert $\left( -2,0 \right)$from Cartesian to polar coordinates? $$$$

Answer 1

We recall the definitions of the polar coordinates $\left( r,\theta \right)$and Cartesian coordinates$\left( x,y \right)$. We find $r$ as the distance between origin and the Cartesian point as $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$ and $\theta$ as the angle the ray joining the origin and the point makes with positive $x-$axis $\theta =\operatorname{atan}2\theta$ where $\operatorname{atan}2\left( y,x \right)$ represents 2-argument inverse tangent function.$$$$

Complete step by step answer:
We know that Cartesian coordinate system the position of the any point on the plane is represented by an ordered pair $\left( x,y \right)$ where the real numbers $x,y$ are the distances from perpendicular reference lines called $x-$axis and $y-$axis. The first number is $x$ is called $x-$coordinate measured whose absolute value is distance from $y-$axis and second number $y$ is called $y-$coordinate whose absolute value is distance from $x-$axis. We also know that in the polar coordinate system every point is represented in the plane with an ordered pair $\left( r,\theta \right)$ where $r$ is the distance from a reference point (conventionally origin) and $\theta $ is the angle from a reference direction (conventionally positive direction of $x-$axis) . The reference point is called the pole and the reference direction is called the polar axis. Here $r$ is called radial coordinate which is always positive and $\theta \in \left[ 0,2\pi \right)$ is called angular coordinate.

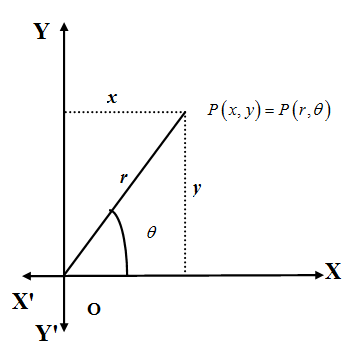
We can convert the Cartesian coordinate $\left( x,y \right)$ to polar coordinate $\left( r,\theta \right)$ of a point using the following relations

& r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\\ & \theta =\operatorname{atan}2\left( y,x \right) \\\ \end{aligned}$$ The function $\operatorname{atan}2\left( y,x \right)$ called 2-argument inverse tangent is defined as follows; $$\theta =\left\\{ \begin{matrix} {{\tan }^{-1}}\left( \dfrac{y}{x} \right) & \text{if }x>0 \\\ {{\tan }^{-1}}\left( \dfrac{y}{x} \right)+\pi & \text{if }x<0\text{ and }y\ge 0 \\\ {{\tan }^{-1}}\left( \dfrac{y}{x} \right)-\pi & \text{if }x<0\text{ and }y<0 \\\ \dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\\ -\dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\\ \text{undefined} & \text{if }x=0\text{ and }y=0 \\\ \end{matrix} \right.$$ We are asked to convert $\left( -2,0 \right)=\left( x,y \right)$ which in Cartesian form to polar form. So we have the radial coordinate as $$r=\sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{{{\left( -2 \right)}^{2}}+0}=\sqrt{4}=2$$ We see that in $\left( -2,0 \right)$ we have $x < 0,y\ge 0$.We find the angular coordinate is using the definition of 2-argument inverse tangent function as $$\operatorname{atan}2\left( \left( -2,0 \right) \right)=\pi +{{\tan }^{-1}}\left( \dfrac{0}{-2} \right)=\pi +{{\tan }^{-1}}\left( 0 \right)=\pi +0=\pi $$ So the polar form of $\left( -2,0 \right)$ is $\left( 2,\pi \right)$ which is drawn below. $$$$  **Note:** We can convert back from polar coordinate $\left( r,\theta \right)$ to Cartesian coordinate $\left( x,y \right)$ using the conversion formula $x=r\cos \theta ,y=r\sin \theta $. We can alternatively find the polar angle $\theta $ as $\theta ={{\sin }^{-1}}\left( \dfrac{x}{r} \right)$. We note that the radial coordinate is always in radian. We also note that negative numbers are not used to represent polar coordinates unlike Cartesian coordinates.