Question

How do you convert $\dfrac{7\pi }{5}$ from radians to degree?

Answer 1

First understand the relation between the real number $\pi$ and the angle corresponding to it in degrees. To do this, assume a circle of unit radius and use the relation: - $\theta =\dfrac{l}{r}$ to establish the required relation between radian and degrees. Once the value of $\pi$ radian is known in terms of degrees, multiply both the sides with $\dfrac{7}{5}$ to get the answer.

Complete step-by-step solution:
Here, we have been provided with the angle $\dfrac{7\pi }{5}$ radian and we have been asked to convert it into degrees. But first we need to know the relation between radian and degrees.
Here, we have been provided with the angle $\dfrac{7\pi }{5}$ radian and we have been asked to convert it into degrees. But first we need to know the relation between radian and degrees.
Now, let us consider a circle with unit radius.

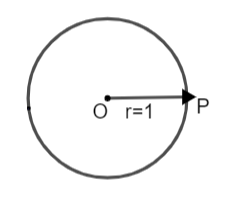
Consider a point P which starts moving on the circumference of this circle. We know that circumference of a circle is given as: - $l=2\pi r$, here ‘l’ can be said as the length of the arc. Since, the radius is 1 unit, so we have,

& \Rightarrow l=2\pi \times 1 \\\ & \Rightarrow l=2\pi \\\ \end{aligned}$$ Using the formula: - $$\theta =\dfrac{l}{r}$$, we get, $$\Rightarrow \theta =\dfrac{2\pi }{1}$$ $$\Rightarrow \theta =2\pi $$ radian Here, $$\theta $$ represents the angle subtended by the initial and final position of the point P at the centre of the circle. Now, when this point P will return at the starting point then it will form an angle of $$2\pi $$ radian but we know that it will form a complete angle, i.e., 360 degrees. So, we can relate the two units of measurement of angle as: - $$\Rightarrow 2\pi $$ radian = 360 degrees Dividing both the sides with 2, we get, $$\Rightarrow \pi $$ radian = 180 degrees – (1) Now, let us come to the question. Here, we have the angle $$\dfrac{7\pi }{5}$$ radian. So, it can be written as: - $$\Rightarrow \dfrac{7\pi }{5}$$ radian = $$\dfrac{7}{5}\times \pi $$ radian Using relation (1), we get, $$\Rightarrow \dfrac{7\pi }{5}$$ radian = $$\left( \dfrac{7}{5}\times 180 \right)$$ degrees On simplifying the R.H.S., we get, $$\Rightarrow \dfrac{7\pi }{5}$$ radian = 252 degrees **Hence, $$\dfrac{7\pi }{5}$$ radian measures 252 degrees.** **Note:** One may note that ‘$$\pi $$’ is a real number and its value is nearly 3.14. So, do not get confused. You don’t need to remember the derivation of the relationship between angle in radian and degrees but you need to remember the result, i.e., $$\pi $$ radian = 180 degrees. Note that these notations are used in higher trigonometry instead of degrees. There is one more unit of angle measurement that is ‘Grad’ but very few books use this notation so we can ignore it.