Question

How do you calculate the left and right Riemann Sum for the given function over the interval $[1,5]$,using $n = 4$ for $f(x) = 3x$?

Answer 1

This sum is a bit difficult if the student is not aware about the concept. Before starting the sum the student should know about the concept of Riemann Sum. A Riemann sum is a certain kind of approximation of an integral by a finite sum. It has two types of sum, Left Riemann Sum(LRS) and Right Riemann sum(RRS). A Right Riemann Sum uses rectangles whose top-right vertices are on the curve.A left Riemann Sum(LRS) uses rectangles whose top-left vertices are on the curve.

Complete Step by Step Solution:
In this sum we will calculate LRS & RRS separately.
It is given $f(x) = 3x$
Also , we have $n = 4$, we want to calculate over the interval $[1,5]$with $4$strips, thus from the given data
$\vartriangle x = \dfrac{{5 - 1}}{4} = 1$
In this particular sum we have a fixed Interval, but a Riemann sum can have a varying size partition width.
The values of the function are as follows:

$x$	$1$	$2$	$3$	$4$	$5$
$f(x)$	$3$	$6$	$9$	$12$	$15$

Left Riemann Sum
LRS = $\sum\limits_{r = 1}^4 {f(x) \times \vartriangle x}$

$\Rightarrow \vartriangle x \times \\{ f(1) + f(2) + f(3) + f(4)\\}$
$\Rightarrow 1 \times \\{ 3 + 6 + 9 + 12\\}$
$\Rightarrow 30$

Right Riemann Sum
RRS =$\sum\limits_{r = 2}^5 {f(x) \times \vartriangle x}$

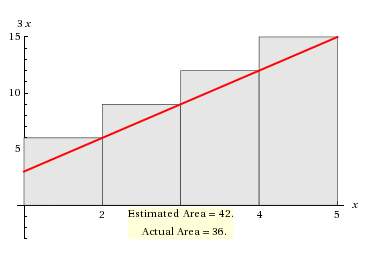
$\Rightarrow \vartriangle x \times \\{ f(2) + f(3) + f(4) + f(5)\\}$
$\Rightarrow 1 \times \\{ 6 + 9 + 12 + 15\\}$
$\Rightarrow 42$
We will have to find out the actual value for comparing the accuracy
Area = $\int\limits_1^5 {3x.dx}$
$= 3 \times {[\dfrac{{{x^2}}}{2}]_1}^5$
$= \dfrac{3}{2} \times ({5^2} - {1^2})$
$= 36$

Thus the Answer for Riemann Sums are
LRS =$30$
RRS= $42$

Note:
The students should know that the Riemann sum is used for approximation. It is used for approximating the area of functions or lines on a graph, but also used for approximations of lengths and other dimensions. The Riemann sum gives an approximate answer and the student should not rely completely on it. If a sum on Riemann sum is asked, the student should always verify the answer by performing integration. Average of LRS & RRS should be close to the value obtained by integration.