Question

How do you calculate the expression $\sin x=0.29$?

Answer 1

We have been given the trigonometric function which is the sine function expressed equivalent to a constant term, 0.29. We know that the sine function is positive in the first as well as the second quadrant of the cartesian plane. Thus, x will have two values out of which one will lie between $\left( 0,{{90}^{\circ }} \right)$ and the other will lie between $\left( {{90}^{\circ }},{{180}^{\circ }} \right)$.

Complete step by step solution:
Given that $\sin x=0.29$. We shall consider the values in the interval $\left( 0,{{180}^{\circ }} \right)$ only as the sine function is positive in the first and second quadrants only.
We know that sine function is an increasing function. It increases from 0 to ${{90}^{\circ }}$ reaching a maximum value of 1 from 0 and decreases from ${{90}^{\circ }}$ to ${{180}^{\circ }}$ reaching 0 from the maximum value of 1.
Now, we shall take the inverse of the given trigonometric function.
$\Rightarrow x={{\sin }^{-1}}\left( 0.29 \right)$
Using trigonometric calculations, we get the value of x as:
$\Rightarrow x\approx {{16.858}^{\circ }}$
Since the sine function is a symmetric function with respect to the x-axis, thus due to symmetry the other value of x will be given as
$\Rightarrow x={{180}^{\circ }}-{{16.858}^{\circ }}$
$\Rightarrow x\approx {{163.142}^{\circ }}$
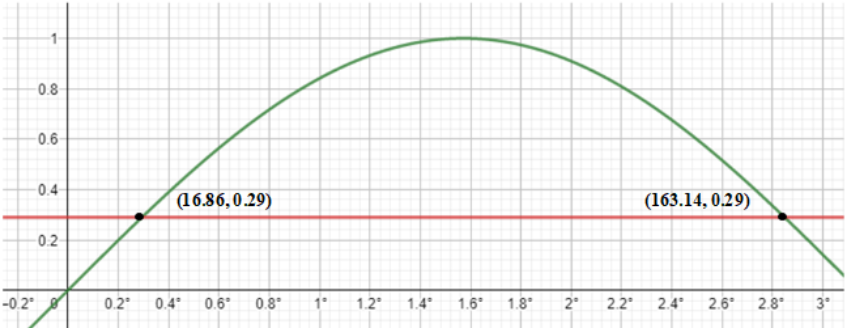
Therefore, for $\sin x=0.29$, $x={{16.86}^{\circ }}$ and ${{163.14}^{\circ }}$.

Note: Another method of solving this problem was by plotting the graph of sine function and the graph of straight-line $y=0.29$ parallel to the x-axis on the same cartesian plane and then marking the points of intersections of these two graphs. The x-coordinate of the points of intersections would give us the solutions of the given expression.