Question

How do you calculate the double integral of $f\left( x,y \right)=28y\left( {{e}^{x}} \right)$ over the triangle indicated by the following points $\left( 0,0 \right),\left( 4,1 \right)$ and $\left( 4,3 \right)$ ?

Answer 1

In this type of questions first we will plot the triangle made from three given points and then we will find the equations of lines used in the triangle and with respect to that equation we will double integrate the given function from lower limit to upper limit using both the axes and we will get the required result.

Complete step-by-step solution:
The given function is $f\left( x,y \right)=28y\left( {{e}^{x}} \right)$
We have to find the value of this function over the triangle formed by these points $\left( 0,0 \right),\left( 4,1 \right)$ and$\left( 4,3 \right)$. First we will plot these points in $XY$ graph and draw a required triangle with the help of points given in the question.

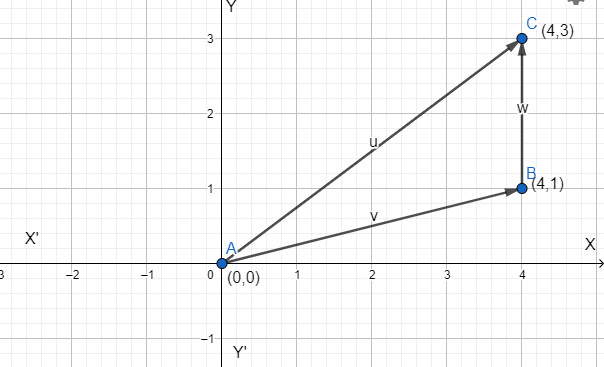
First we will find the equation of line AC and AB.
So Equation of line AC can be calculated as,
First we will find the slope of Line AC
${{m}_{1}}=\dfrac{3}{4}$
So, equation of line AC is
$y=mx+c$.
Here intercept on y axis is zero.
Put the values in these equations we get,
$y=\dfrac{3}{4}x$(Equation 1)
Now we will find the equation of line AB
First we will find the slope of Line AB
${{m}_{2}}=\dfrac{1}{4}$
So, equation of line AB is
$y=mx+c$
Here intercept on y axis is zero.
Put the values in these equations we get,
$y=\dfrac{1}{4}x$(Equation 2)
Now calculate the double integral over the triangle we will do the double integration of the given function.
$x$Function is integrated from lower limit $0$to upper limit $4$
$y$Function is integrated from lower limit $\dfrac{1}{4}x$ to upper limit$\dfrac{3}{4}x$.
So integration of given function can be done as,
$\int\limits_{0}^{4}{\int\limits_{\dfrac{1}{4}x}^{\dfrac{3}{4}x}{28y({{e}^{x}})dydx}}$
$= \int\limits_{0}^{4}{28{{e}^{x}}dx\left[ \dfrac{{{y}^{2}}}{2} \right]_{\dfrac{1}{4}x}^{\dfrac{3}{4}x}}$

& = \int\limits_{0}^{4}{28{{e}^{x}}dx\dfrac{1}{2}\left[ \dfrac{9}{16}{{x}^{2}}-\dfrac{1}{16}{{x}^{2}} \right]} \\\ & = \int\limits_{0}^{4}{28{{e}^{x}}dx\dfrac{1}{2}{{x}^{2}}\left[ \dfrac{9}{16}-\dfrac{1}{16} \right]} \\\ \end{aligned}$$ $$= \int\limits_{0}^{4}{28{{e}^{x}}dx\dfrac{1}{2}{{x}^{2}}\left[ \dfrac{8}{16} \right]}$$ On Simplifying we get, $$= 28\int\limits_{0}^{4}{\dfrac{1}{4}{{e}^{x}}{{x}^{2}}dx}$$ $$= 7\int\limits_{0}^{4}{{{e}^{x}}{{x}^{2}}dx}$$ Now apply integration by parts on above integral, we get $$= 7{{\left[ {{x}^{2}}\int{{{e}^{x}}dx}-\int{\left( \dfrac{d}{dx}{{x}^{2}}\int{{{e}^{x}}dx} \right)dx} \right]}^{4}}_{0}$$ $$= 7\left[ {{x}^{2}}{{e}^{x}}-\int{\left( 2x{{e}^{x}} \right)dx} \right]_{0}^{4}$$ Now again we have to apply integration by parts on above integral we get, $$\begin{aligned} & = 7\left[ {{x}^{2}}{{e}^{x}}-2\left\\{ x{{e}^{x}}-{{e}^{x}} \right\\} \right]_{0}^{4} \\\ & = 7\left[ {{x}^{2}}{{e}^{x}}-2x{{e}^{x}}+2{{e}^{x}} \right]_{0}^{4} \\\ \end{aligned}$$ Now put the values of upper limit and lower limit in the above function, we get $$= 7\left[ (16{{e}^{4}}-8{{e}^{4}}+2{{e}^{4}})-(0-0+2) \right]$$ On simplifying we get the value of integration. $$\therefore 7\left[ 10{{e}^{4}}-2 \right]$$. So the value of double integral of $f\left( x,y \right)=28y\left( {{e}^{x}} \right)$ over the triangle indicated by the following points $\left( 0,0 \right),\left( 4,1 \right)$ and $\left( 4,3 \right)$ is given as$$7\left[ 10{{e}^{4}}-2 \right]$$. **Note:** Integration has much significance in field of mathematics; they are used to find the area of any closed figure or area under a curve or area between two curves ,it is also used to find the average value of curve , it also has much significance in field of physics as integration is used to find the centre of mass of body.