Solveeit Logo
Login

Question

Question: How do you calculate \(\cos \left( {{\tan }^{-1}}\dfrac{4}{3}-{{\sin }^{-1}}\dfrac{12}{13} \right)\)...

How do you calculate cos⁡(tan⁡−143−sin⁡−11213)\cos \left( {{\tan }^{-1}}\dfrac{4}{3}-{{\sin }^{-1}}\dfrac{12}{13} \right) ?

Explanation

Solution

We recall the range of tangent inverse, sine inverse function. We take A=tan⁡−143,B=sin⁡−11213A={{\tan }^{-1}}\dfrac{4}{3},B={{\sin }^{-1}}\dfrac{12}{13} and use the cosine difference of angle formula cos⁡(A−B)=cos⁡Acos⁡B+sin⁡Asin⁡B\cos \left( A-B \right)=\cos A\cos B+\sin A\sin B. We find scos⁡A,cos⁡B,sin⁡A,sin⁡Bs\cos A,\cos B,\sin A,\sin B using the ratios of right angled triangles.

Complete step by step answer:

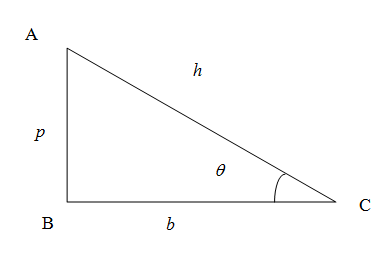
We know that in the right angled triangle the side opposite to the right angled triangle is called hypotenuse denoted as hh, the vertical side is called perpendicular denoted as pp and the horizontal side is called the base denoted as bb.
We know from the trigonometric ratios in a right angled triangle the sine of any angle is given by the ratio of side opposite to the angle to the hypotenuse, cosine of an angle is the ratio of side adjacent to the angle (excluding hypotenuse) to the hypotenuse and tangent of the angle is the ratio of opposite side to the adjacent side (excluding hypotenuse) . So we have
sin⁡θ=ph,cos⁡θ=bh,tan⁡θ=pb\sin \theta =\dfrac{p}{h},\cos \theta =\dfrac{b}{h},\tan \theta =\dfrac{p}{b}
We use Pythagoras thrum to have theorem to have;
p2+b2=h2{{p}^{2}}+{{b}^{2}}={{h}^{2}}
We know that range of tangent inverse function is (−π2,π2)\left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right) and range of sine inverse function is [−π2,π2]\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right].We are asked to evaluate the following expression
cos⁡(tan⁡−143−sin⁡−11213)\cos \left( {{\tan }^{-1}}\dfrac{4}{3}-{{\sin }^{-1}}\dfrac{12}{13} \right)
Let us assumeA=tan⁡−143,B=sin⁡−11213A={{\tan }^{-1}}\dfrac{4}{3},B={{\sin }^{-1}}\dfrac{12}{13}.So we have
⇒cos⁡(A−B)\Rightarrow \cos \left( A-B \right)
We use cosine difference of angle formula to have;
⇒cos⁡(A−B)=cos⁡Acos⁡B+sin⁡Asin⁡B.......(1)\Rightarrow \cos \left( A-B \right)=\cos A\cos B+\sin A\sin B.......\left( 1 \right)
We take tangent both sides of A=tan⁡−143A={{\tan }^{-1}}\dfrac{4}{3}to have tan⁡A=tan⁡(tan⁡−143)=43\tan A=\tan \left( {{\tan }^{-1}}\dfrac{4}{3} \right)=\dfrac{4}{3}. If we take p=4,b=3p=4,b=3 in right angled triangle to have h=p2+b2=42+32=5h=\sqrt{{{p}^{2}}+{{b}^{2}}}=\sqrt{{{4}^{2}}+{{3}^{2}}}=5. So we have
sin⁡A=ph=45,cos⁡A=bh=35\sin A=\dfrac{p}{h}=\dfrac{4}{5},\cos A=\dfrac{b}{h}=\dfrac{3}{5}
We take sine of both sides B=sin⁡−11213B={{\sin }^{-1}}\dfrac{12}{13} to have sin⁡B=1213\sin B=\dfrac{12}{13}. If we take p=12,h=13p=12,h=13 we have b=h2−p2=132−122=5b=\sqrt{{{h}^{2}}-{{p}^{2}}}=\sqrt{{{13}^{2}}-{{12}^{2}}}=5 to have
cos⁡B=bh=513\cos B=\dfrac{b}{h}=\dfrac{5}{13}
We put sin⁡A=45,cos⁡A=35,sin⁡B=1213,cos⁡B=513\sin A=\dfrac{4}{5},\cos A=\dfrac{3}{5},\sin B=\dfrac{12}{13},\cos B=\dfrac{5}{13} in (1) to have the required value
cos⁡(A−B)=35⋅513+45⋅1213=1565+4865=6365\cos \left( A-B \right)=\dfrac{3}{5}\cdot \dfrac{5}{13}+\dfrac{4}{5}\cdot \dfrac{12}{13}=\dfrac{15}{65}+\dfrac{48}{65}=\dfrac{63}{65}

Note:
We note that the domain of sine inverse function is [−1,1]\left[ -1,1 \right] and since 1213∈[−1,1]\dfrac{12}{13}\in \left[ -1,1 \right] the value sin⁡−11213{{\sin }^{-1}}\dfrac{12}{13} is well defined. The domain of tangent inverse function is real number set and hence tan⁡−143{{\tan }^{-1}}\dfrac{4}{3} is well defined. We can alternatively use Pythagorean trigonometric identities cos⁡θ=1−sin⁡2θ,sin⁡θ=1−cos⁡2θ\cos \theta =\sqrt{1-{{\sin }^{2}}\theta },\sin \theta =\sqrt{1-{{\cos }^{2}}\theta } and sin⁡θ=tan⁡θcos⁡θ\sin \theta =\tan \theta \cos \theta to find the values of cos⁡B,sin⁡B,sin⁡A\cos B,\sin B,\sin A,