Solveeit Logo
Login

Question

Question: How do you calculate \(\cos \left( {{{\tan }^{ - 1}}\left( {\dfrac{3}{4}} \right)} \right)\) ?...

How do you calculate cos⁡(tan⁡−1(34))\cos \left( {{{\tan }^{ - 1}}\left( {\dfrac{3}{4}} \right)} \right) ?

Explanation

Solution

Here the basic concept which is going to be used is that we can convert arctan into arccos. So, firstly we will convert the value tan⁡−1(34){\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right) into arccos and then we will just adjust the value, that was left behind, with cosine.

Complete Step by Step Solution:
We have to find the value of cos⁡(tan⁡−1(34))\cos \left( {{{\tan }^{ - 1}}\left( {\dfrac{3}{4}} \right)} \right)
So, now let us consider tan⁡−1(34){\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right) as θ\theta
⇒tan⁡−1(34)=θ\Rightarrow {\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right) = \theta ……(i)
Now, we will multiply both sides by tan, then we will get
⇒tan⁡(tan⁡−1(34))=tan⁡θ\Rightarrow \tan \left( {{{\tan }^{ - 1}}\left( {\dfrac{3}{4}} \right)} \right) = \tan \theta
Now, we will adjust tan with tan⁡−1{\tan ^{ - 1}} on the left side, then we will get
⇒tan⁡θ=34\Rightarrow \tan \theta = \dfrac{3}{4}
As we know that tan⁡θ=PB\tan \theta = \dfrac{P}{B}, where P is perpendicular and B is the base of a right angle triangle
Let us take hypotenuse as H. Now we will apply Pythagoras theorem i.e. H2=P2+B2{H^2} = {P^2} + {B^2}
Here P and B are 3 and 4 respectively
So, H2=P2+B2{H^2} = {P^2} + {B^2}
⇒H2=32+42\Rightarrow {H^2} = {3^2} + {4^2}
On further simplification,
⇒H2=9+16\Rightarrow {H^2} = 9 + 16
⇒H2=25\Rightarrow {H^2} = 25
Now, take the square root of both sides
⇒H2=25\Rightarrow \sqrt{{{H}^{2}}}=\sqrt{25}
⇒H=5\Rightarrow H = 5

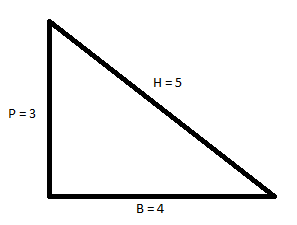
Now, as we know that cos⁡θ=BH\cos \theta = \dfrac{B}{H}
Therefore, cos⁡θ=45\cos \theta = \dfrac{4}{5}
From (i), we can see that θ=tan⁡−1(34)\theta = {\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right)

Hence, cos⁡(tan⁡−1(34))=45\cos \left( {{{\tan }^{ - 1}}\left( {\dfrac{3}{4}} \right)} \right) = \dfrac{4}{5}
⇒cos⁡(tan⁡−1(34))=0.8\Rightarrow \cos \left( {{{\tan }^{ - 1}}\left( {\dfrac{3}{4}} \right)} \right) = 0.8

Note:
It will be suggested to you that whenever you are doing these types of questions, just simply make a right angle triangle. Mark hypotenuse, perpendicular, and base on it and write the value in front of it so that you will not make any kind of mistake. And one more thing, take care that the trigonometric function is the ratio of perpendicular and hypotenuse, base and hypotenuse, perpendicular and base.