Question

How do we find the latus rectum of the parabola $y = 2{x^2}$ .

Answer 1

We are given the equation of a parabola and we have to find the length of its latus rectum.
So, first, we will find the end coordinates of the latus rectum, and then using the distance formula, we will find its length.
General equation of parabola: ${\left( {x - h} \right)^2} = 4a\left( {y - k} \right)$ , where, $\left( {h,k} \right)$ in the center of the parabola and $a$ is the focal length.
Distance between the points $\left( {{x_1},{x_2}} \right)$ and $\left( {{y_1},{y_2}} \right)$ is given by $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$ .

Complete step by step answer:
Given the equation of the parabola: $y = 2{x^2}$ .
To find the length of the latus rectum of the parabola.
Let the endpoints of the latus rectum of the parabola be $L$ and $L'$ .
First, we will find these coordinates then their length.
Let $L = \left( {b,a} \right)$ , the $y -$ coordinate is equivalent to $'a'$ . i.e., $L = \left( {0,a} \right)$ and since, $L$ is a point on the parabola, therefore, it satisfies the equation of a parabola, i.e., ${b^2} = 4{a^2}$ .
Taking square root, gives, $b = \pm 2a$ .
Thus, the endpoints of the latus rectum of the parabola are $L = \left( {2a,a} \right)$ and $L' = \left( { - 2a,a} \right)$ .
Now, the length of the latus rectum is given $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} - {{\left( {{y_2} - {y_1}} \right)}^2}}$ .
Putting values, we get, $= \sqrt {{{\left( { - 2a - 2a} \right)}^2} - {{\left( {a - a} \right)}^2}}$ .
On solving, we get, length of the latus rectum $= 4a$ .
Now, comparing the given equation with the general equation of a parabola, we get,
$a = \dfrac{1}{8}$ , as shown in the figure below,

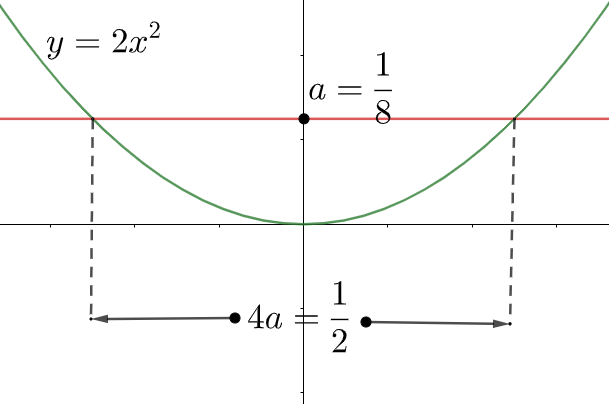
Therefore, the length of the latus rectum of the parabola $= 4a = 4 \times \dfrac{1}{8} = \dfrac{1}{2}$.

Note: In general, the length of the latus rectum of a parabola is $4a$ , where, $a$ is the focal length.
In the conic section, the latus rectum is the chord drawn from the focus and is parallel to the directrix.
In general, there are 4 types of parabolas, with equations $y = \pm 4a{x^2}$ and $x = \pm 4a{y^2}$ .