Question

How do solve $\cos 2x=2\cos x-1$ in the interval $\left[ 0,2\pi \right]$ ?

Answer 1

At first, we apply the formula $\cos 2x=2{{\cos }^{2}}x-1$ . We get a quadratic in $\cos x$ . We then apply the Sridhar Acharya formula to get the roots of $\cos x$ in the interval $\left[ 0,2\pi \right]$ .

Complete step by step solution:
The given equation is
$\cos 2x=2\cos x-1$
If we carefully observe the above equation, we can see that if we can express $\cos 2x$ in terms of $\cos x$ , then the equation becomes an equation of $\cos x$ . Luckily, we have a formula between $\cos 2x$ and $\cos x$ which is,
$\cos 2x=2{{\cos }^{2}}x-1$
Putting this value of $\cos 2x$ in the given equation, the equation thus becomes,
$\Rightarrow 2{{\cos }^{2}}x-1=2\cos x-1$
Now, we subtract $2\cos x$ from both sides of the above equation and get,
$\Rightarrow 2{{\cos }^{2}}x-2\cos x-1=-1$
Now, we cancel $1$ from both sides of the above equation and get,
$\Rightarrow 2{{\cos }^{2}}x-2\cos x=0$
We now divide the entire equation by $2$ and get,
$\Rightarrow {{\cos }^{2}}x-\cos x=0$
This is nothing but a quadratic equation in $\cos x$ . Let us take $\cos x=z$ . We then rewrite the entire equation as,
$\Rightarrow {{z}^{2}}-z=0$
Thus, the quadratic equation has transformed into a quadratic equation in $z$ . So, we now need to solve for $z$ by solving this quadratic. We apply the Sridhar Acharya formula which is
$z=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
In our problem, $a=1,b=-1,c=0$ . So, putting these values in the formula, we get,
$\begin{aligned} & \Rightarrow z=\dfrac{-\left( -1 \right)\pm \sqrt{{{\left( -1 \right)}^{2}}-4\left( 0 \right)}}{2} \\\ & \Rightarrow z=\dfrac{1\pm 1}{2} \\\ & \Rightarrow z=\dfrac{1}{2}\pm \dfrac{1}{2} \\\ \end{aligned}$
So, we get two roots of $z$ which are $\dfrac{1}{2}+\dfrac{1}{2}=1$ and $\dfrac{1}{2}-\dfrac{1}{2}=0$ . But, $z=\cos x$ . This means, $\cos x$ has two roots,
$\begin{aligned} & \cos x=1...\left( 1 \right) \\\ & \cos x=0...\left( 2 \right) \\\ \end{aligned}$
$\left( 1 \right)$ gives $x={{\cos }^{-1}}1$ which gives the values $0,2\pi$ within $\left[ 0,2\pi \right]$ .
$\left( 2 \right)$ gives $x={{\cos }^{-1}}0$ which gives the values $\dfrac{\pi }{2},\dfrac{3\pi }{2}$ within $\left[ 0,2\pi \right]$ .

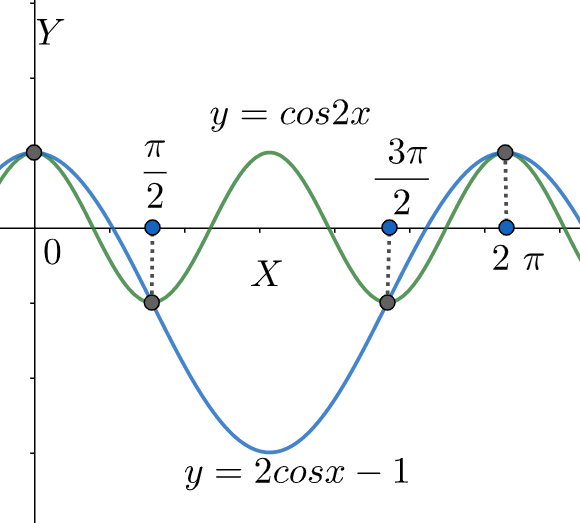
Therefore, we can conclude that the values of $x$ in $\left[ 0,2\pi \right]$ which satisfy the given equation are $0,\dfrac{\pi }{2},\dfrac{3\pi }{2},2\pi$.

Note: We should be careful while solving the quadratic equation in $\cos x$ and should apply the Sridhar Acharya formula correctly. This equation can also be solved by taking two equations $y=\cos 2x$ and $y=2\cos x-1$ . The points where two curves intersect in $\left[ 0,2\pi \right]$ will be the required answers.