Question

How do I use the completing square to describe the graph of the function $f\left( x \right)=30-12x-{{x}^{2}}$?

Answer 1

Now we know that the quadratic equation represents a parabola. Also we know that if a < 0 then the parabola is downwards facing. Now we will find the axis of symmetry by $x=\dfrac{-b}{2a}$ and the intercept by substituting x = 0 in the equation. Now we will find the roots of the equation by using the completing square method and hence plot the graph of the given function.

Complete step by step solution:
Now first consider the given function $f\left( x \right)=30-12x-{{x}^{2}}$ .
Now the given function is a quadratic function of the form $a{{x}^{2}}+bx+c$ where a = -1, b = -12 and c = 30.
Now we know that the equation $a{{x}^{2}}+bx+c$ represents a parabola. Also the parabola is upwards facing if a > 0 and downwards facing if a < 0. Hence the given function represents a downwards facing parabola. Now also we know that the axis of symmetry lies at $x=\dfrac{-b}{2a}$ Hence the axis of symmetry is $x=\dfrac{12}{2\left( 30 \right)}=\dfrac{1}{5}$ .
Now on substituting x = 0 in the equation we get $f\left( x \right)= 30$ . Hence the intercept of the function is $\left( 0, -30 \right)$
Now let us find the roots of the expression.
To find the roots of the expression we will use completing the square method.
First consider the equation $30-12x-{{x}^{2}}=0$
Rearranging the terms of the equation we get, ${{x}^{2}}+12x=30$ .
Now let us add ${{\left( \dfrac{b}{2a} \right)}^{2}}$ on both side we get,
$\Rightarrow {{x}^{2}}+12x+{{\left( 6 \right)}^{2}}=30+{{6}^{2}}$
Now using the formula ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ we get,
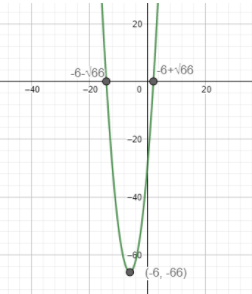
$\Rightarrow {{\left( x+6 \right)}^{2}}=66$
Now taking square root in both sides $x+6=\pm \sqrt{66}$
Hence the roots of the equation are $x=-6\pm \sqrt{66}$
Now let us draw the graph of the equation.

Note: Now note that we can directly find the root of the equation by using the formula for roots of quadratic equation. The roots of quadratic equation of the form $a{{x}^{2}}+bx+c$ is given by $\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ . Also note that the roots can be real repeating or complex depending on the value of Discriminant which is given by ${{b}^{2}}-4ac$.