Question

How do I use DeMoivre's theorem to find out ${{\left( -3+3i \right)}^{3}}$?

Answer 1

To solve this complex expression, first assume $z=-3+3i$ and then change this complex number into trigonometric form that is $z=\rho \left[ \cos \left( \theta \right)+i\sin \left( \theta \right) \right]$ and then apply DeMoivre’s theorem which is ${{z}^{n}}={{\rho }^{n}}\left[ \cos \left( n\theta \right)+i\sin \left( n\theta \right) \right]$ to get the value of ${{z}^{3}}={{\left( -3+3i \right)}^{3}}$.

Complete step by step solution:
Let us suppose given complex number to be as follows:
$z=-3+3i$
$\Rightarrow {{z}^{3}}={{\left( -3+3i \right)}^{3}}$
To change this complex number into trigonometric form that is
$z=\rho \left[ \cos \left( \theta \right)+i\sin \left( \theta \right) \right]...\left( 1 \right)$
we need to find the value of $\theta$ and $\rho$ . We know that $\rho =\sqrt{{{\left( x \right)}^{2}}+{{\left( y \right)}^{2}}}$here $x=-3$ and $y=3$. After applying these values, we get:
$\Rightarrow \rho =\sqrt{{{\left( -3 \right)}^{2}}+{{\left( 3 \right)}^{2}}}$
$\Rightarrow \rho =\sqrt{9+9}$
$\Rightarrow \rho =3\sqrt{2}$
To find the value of $\theta$ formula is $\theta =\arctan \left( \dfrac{y}{x} \right)$ here $x=-3$ and $y=3$. After applying these values, we get:
$\Rightarrow \theta =\arctan \left( \dfrac{3}{-3} \right)$
$\Rightarrow \theta =\arctan \left( -1 \right)$
$\Rightarrow \theta =\dfrac{3\pi }{4}$
Now substitute the value of $\theta$ and $\rho$ in equation $\left( 1 \right)$ to convert in trigonometry form we get:
$\Rightarrow z=3\sqrt{2}\left[ \cos \left( \dfrac{3\pi }{4} \right)+i\sin \left( \dfrac{3\pi }{4} \right) \right]$
And apply DeMoivre’s theorem which is ${{z}^{n}}={{\rho }^{n}}\left[ \cos \left( n\theta \right)+i\sin \left( n\theta \right) \right]$ in equation ${{z}^{3}}={{\left( -3+3i \right)}^{3}}$ we get:
$\Rightarrow {{z}^{3}}={{\left( 3\sqrt{2} \right)}^{3}}\left[ \cos \left( 3\cdot \dfrac{3\pi }{4} \right)+i\sin \left( 3\cdot \dfrac{3\pi }{4} \right) \right]$
$\Rightarrow {{z}^{3}}={{\left( 3\sqrt{2} \right)}^{3}}\left[ \cos \left( \dfrac{9\pi }{4} \right)+i\sin \left( \dfrac{9\pi }{4} \right) \right]$
$\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \cos \left( \dfrac{9\pi }{4} \right)+i\sin \left( \dfrac{9\pi }{4} \right) \right]$
We can further split this angle as $\dfrac{9\pi }{4}=2\pi +\dfrac{\pi }{4}$ and replace it in the above equation we get:
$\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \cos \left( 2\pi +\dfrac{\pi }{4} \right)+i\sin \left( 2\pi +\dfrac{\pi }{4} \right) \right]$
According to the one of the trigonometric properties of cosine and sine one of them is $\cos \left( 2\pi +\theta \right)=\cos \left( \theta \right)$ and $\sin \left( 2\pi +\theta \right)=\sin \left( \theta \right)$ using these in the above equation we get:
$\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \cos \left( \dfrac{\pi }{4} \right)+i\sin \left( \dfrac{\pi }{4} \right) \right]$
We know that value of $\cos \left( \dfrac{\pi }{4} \right)=\sin \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}$, by substituting this value we get:
$\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \dfrac{1}{\sqrt{2}}+i\dfrac{1}{\sqrt{2}} \right]$
Now we take LCM within the brackets and simplify we get:
$\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \dfrac{1+i}{\sqrt{2}} \right]$
As we can see $\sqrt{2}$ is there in both numerator and denominators. So, it gets cancelled. Hence, we are left with the following:
$\Rightarrow {{z}^{3}}=54\left[ 1+i \right]$
After solving the bracket, we get:
$\Rightarrow {{z}^{3}}=54+54i$
Therefore, value of ${{z}^{3}}={{\left( -3+3i \right)}^{3}}$ is ${{z}^{3}}=54+54i$.

Note:
Students can go wrong by using wrong DeMoivre’s formula that is some students use ${{z}^{n}}={{\rho }^{n}}\left[ n\cos \left( \theta \right)+n\sin \left( \theta \right)i \right]$ instead of ${{z}^{n}}={{\rho }^{n}}\left[ \cos \left( n\theta \right)+i\sin \left( n\theta \right) \right]$ which further leads to the wrong result. Hence, it’s important to remember DeMoivre’s theorem which is ${{z}^{n}}={{\rho }^{n}}\left[ \cos \left( n\theta \right)+i\sin \left( n\theta \right) \right]$ right. Also, you can find the value of $\theta$ by observing the graph of given complex no. that is:

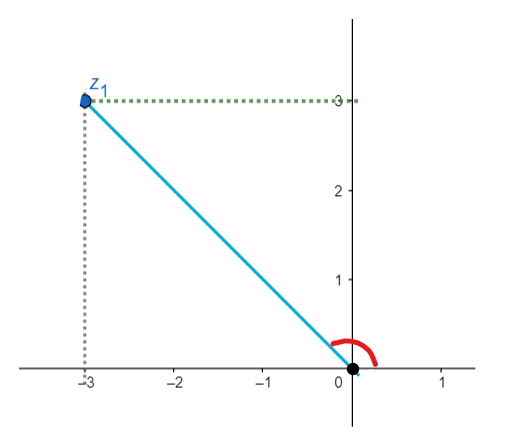
Clearly you can see the angle is equal to $\dfrac{\pi }{2}+\dfrac{\pi }{4}=\dfrac{3\pi }{4}$. Which implies $\theta =\dfrac{3\pi }{4}$