Question

How do I solve this? An airplane heads $N60^{\circ} E$ at $60 mph$ in still air. A tail wind begins to blow in the direction $N30^{\circ} E$ at $50 mph$. Find the resulting speed of the airplane and its resulting direction of travel. Draw a diagram.

Answer 1

Airplane speed in air and wind speed is given then due to wind, relative speed of aeroplane is to be found and the theta angle gives the direction in which aeroplane moves with east. First take the component of aeroplane speed and wind speed along the x axis and y axis. After getting the components, resultant speed can determine.

Complete answer:
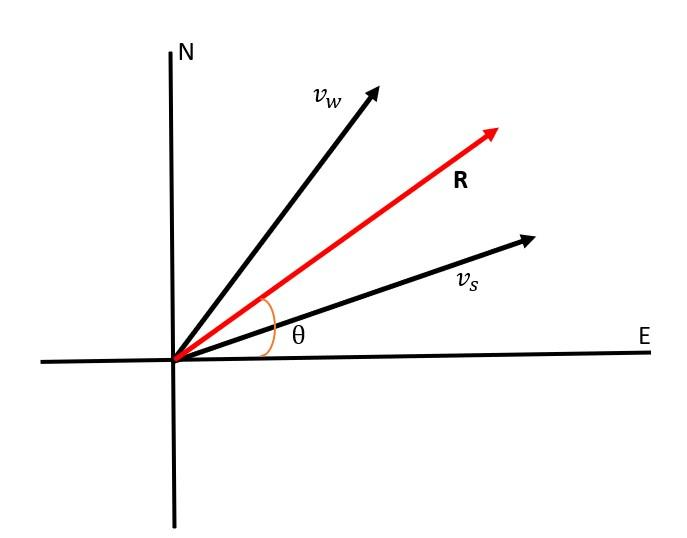
Let’s first understand what is $N60^{\circ} E$. It means we go $60^{\circ}$ towards east from reference north direction.
$N30^{\circ} E$ means wind goes $60^{\circ}$ towards east from reference north direction.
Now take east as $+x$ direction and north as $+y$ direction.
As such airplane's speed $v_{s}$ in still air makes an angle of $30^{\circ}$ with the axis and tail wind $v_{w}$ makes an angle of $60^{\circ}$ with it.
Let R be resultant of both. Resolving all there along the x and y axes and equating both we get, for components along x axis: -
$R_{x} = v_{sx} + v_{wx}$
$\implies R_{x} = 600 cos 30^{\circ} + 50 cos 60^{\circ}$
$\implies R_{x} = 600 \dfrac{\sqrt{3}}{2} + 50 \dfrac{1}{2}$
$\implies R_{x} = 519.62 mph$
Similarly, for components along y axis: -
$R_{y} = v_{sy} + v_{wy}$
$\implies R_{y} = 600 sin 30^{\circ} + 50 sin 60^{\circ}$
$\implies R_{y} = 600 \dfrac{1}{2} + 50 \dfrac{\sqrt{3}}{2}$
$\implies R_{y} = 343.50 mph$
Now, $R = \sqrt{ R_{x}^{2} + R_{y}^{2}}$
$\implies R = \sqrt{ 519.62^{2} + 343.50^{2}}$
$\implies R = 622.8 mph$
If $\theta$ is the angle made by resultant with x axis then
$\theta = tan^{-1} \left(\dfrac{R_{y}}{R_{x}}\right)$
$\implies \theta = tan^{-1} \left(\dfrac{343.50}{519.62 }\right)$
$\implies \theta = 33.5^{\circ}$
This can also be written as $N56.5^{\circ} E$.

Additional Information:
For relative Speed, one body can be made stationary and take the other body's Speed with respect to the stationary body, which is the sum of the speeds if the bodies move in the opposite direction and the difference moving in the same direction. This Speed of the moving body with respect to the stationary body is called the relative Speed.

Note:
Relative speed of a body is defined as the speed of a moving body with respect to another. Angle is given with the y axis, for finding the x component, we need to find the angle with the x axis. For angle along x axis, we to subtract the y axis angle from $90^{\circ}$.