Solveeit Logo
Login

Question

Question: How do I solve \(4\sin x + 9\cos x = 0\) for \(0 < x < {360^ \circ }\)?...

How do I solve 4sin⁡x+9cos⁡x=04\sin x + 9\cos x = 0 for 0<x<360∘0 < x < {360^ \circ }?

Explanation

Solution

First, subtract 9cos⁡x9\cos x from both sides of the equation. Then, divide both sides of the equation by 4cos⁡x4\cos x and simplify using trigonometry identities. Then, find the value of xx satisfying tan⁡x=−94\tan x = - \dfrac{9}{4} using trigonometric properties. Next, find all values of xx in the interval 0<x<360∘0 < x < {360^ \circ }. Then, we will get all the solutions of the given equation in the given interval.
Formula used:
tan⁡θ=sin⁡θcos⁡θ\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}
tan⁡−1(94)=1.15{\tan ^{ - 1}}\left( {\dfrac{9}{4}} \right) = 1.15
tan⁡(π−x)=−tan⁡x\tan \left( {\pi - x} \right) = - \tan x
tan⁡(2π−x)=−tan⁡x\tan \left( {2\pi - x} \right) = - \tan x

Complete step by step answer:
Given equation: 4sin⁡x+9cos⁡x=04\sin x + 9\cos x = 0
We have to find all possible values of xx satisfying a given equation in the interval 0<x<360∘0 < x < {360^ \circ }.
First, subtract 9cos⁡x9\cos x from both sides of the equation.
4sin⁡x=−9cos⁡x4\sin x = - 9\cos x
Divide both sides of the equation by 4cos⁡x4\cos x, we get
sin⁡xcos⁡x=−94\dfrac{{\sin x}}{{\cos x}} = - \dfrac{9}{4}
Now, use the identity tan⁡θ=sin⁡θcos⁡θ\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }} in the above equation.
⇒tan⁡x=−94\Rightarrow \tan x = - \dfrac{9}{4}
Now, we will find the values of xx satisfying tan⁡x=−94\tan x = - \dfrac{9}{4}…(i)
So, using the property tan⁡(π−x)=−tan⁡x\tan \left( {\pi - x} \right) = - \tan x and tan⁡−1(94)=1.15{\tan ^{ - 1}}\left( {\dfrac{9}{4}} \right) = 1.15 in equation (i).
⇒tan⁡(x)=−tan⁡(1.15)\Rightarrow \tan \left( x \right) = - \tan \left( {1.15} \right)
⇒tan⁡(x)=tan⁡(3.14−1.15)\Rightarrow \tan \left( x \right) = \tan \left( {3.14 - 1.15} \right)
⇒x=1.99\Rightarrow x = 1.99
Now, using the property tan⁡(2π−x)=−tan⁡x\tan \left( {2\pi - x} \right) = - \tan x and tan⁡−1(94)=1.15{\tan ^{ - 1}}\left( {\dfrac{9}{4}} \right) = 1.15 in equation (i).
⇒tan⁡(x)=−tan⁡(1.15)\Rightarrow \tan \left( x \right) = - \tan \left( {1.15} \right)
⇒tan⁡(x)=tan⁡(2×3.14−1.15)\Rightarrow \tan \left( x \right) = \tan \left( {2 \times 3.14 - 1.15} \right)
⇒x=5.13\Rightarrow x = 5.13
Since, the period of the tan⁡(x)\tan \left( x \right) function is π\pi so values will repeat every π\pi radians in both directions.
x=1.99+nπ,5.13+nπx = 1.99 + n\pi ,5.13 + n\pi , for any integer nn.
Now, find all values of xx in the interval 0<x<360∘0 < x < {360^ \circ }.
Since, it is given that x∈(0,6.28)x \in \left( {0,6.28} \right), hence put n=0n = 0 in the general solution.
So, putting n=0n = 0 in the general solution, x=1.99+nπ,5.13+nπx = 1.99 + n\pi ,5.13 + n\pi , we get
∴x=1.99,5.13\therefore x = 1.99,5.13
Final solution: Hence, x=1.99,5.13x = 1.99,5.13 are the solutions of the given equation in the given interval.

Note:
In above question, we can find the solutions of given equation by plotting the equation, 4sin⁡x+9cos⁡x=04\sin x + 9\cos x = 0 on graph paper and determine all solutions which lie in the interval, 0<x<360∘0 < x < {360^ \circ }.

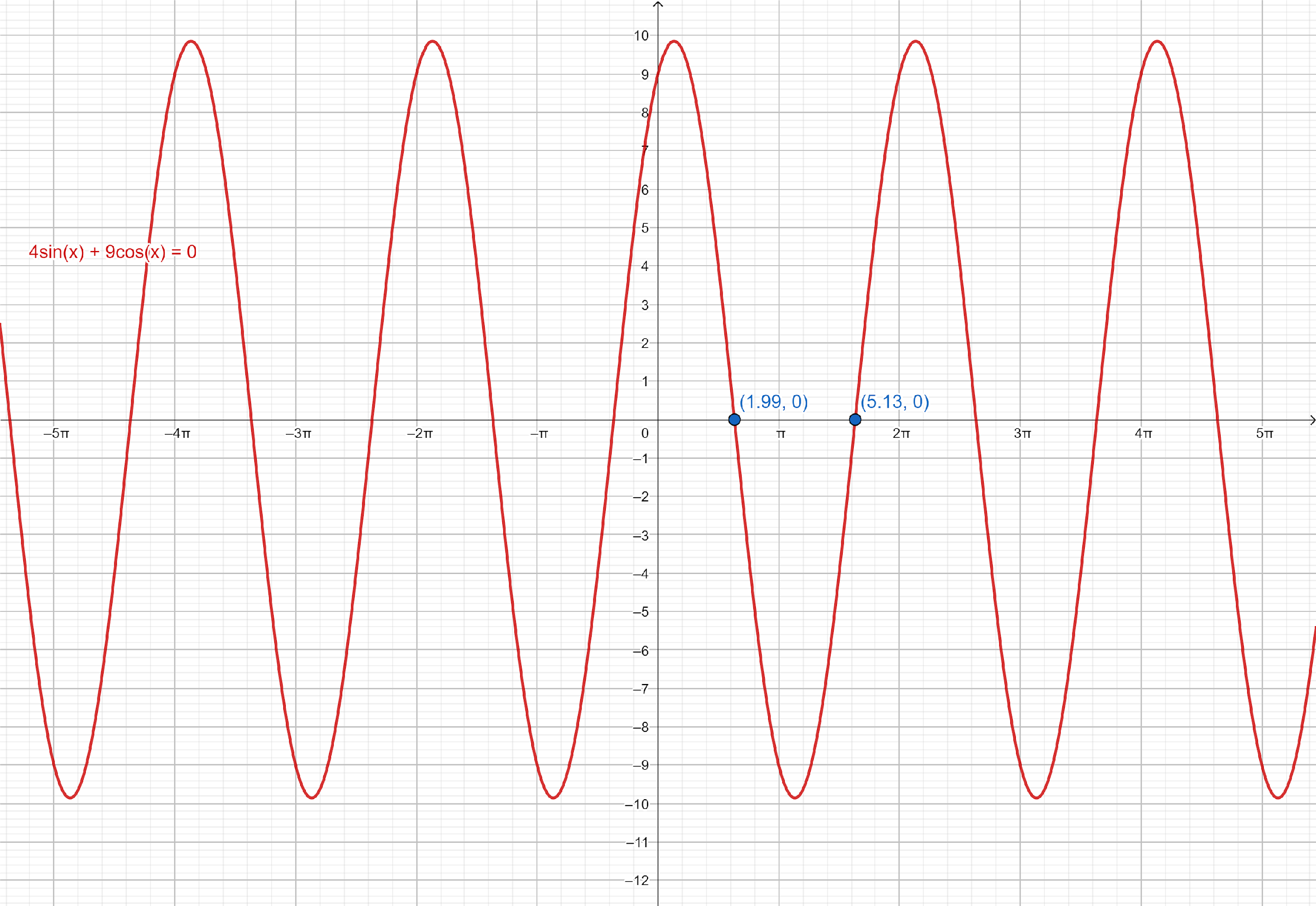
From the graph paper, we can see that there are two values of xx in the interval 0<x<360∘0 < x < {360^ \circ }.
So, these will be the solutions of the given equation in the given interval.
Final solution: Hence, x=1.99,5.13x = 1.99,5.13 are the solutions of the given equation in the given interval.