Question

How do I multiply a vector by a scalar?

Answer 1

To multiply a vector by a scalar, just multiply the same or comparable parts, that is, the vector's size(magnitude) by the scalar's size. This will bring out another vector which is the product of the two given magnitudes, and which is heading in the same direction.

Complete step-by-step solution:
The terms vectors and scalars represent different types of physical quantities.
Vector, in mathematics and physics, is a quantity that has both a magnitude and a direction.
Whereas a scalar is a quantity that solely has only magnitude and has no direction.
Hence when it is necessary for them to interact, the only possible method is multiplication because adding a scalar to a vector is impossible due to their various measurements in space.
Moreover, it is possible to multiply a vector by a scalar. A scalar, be that as it may, cannot be multiplied by a vector.
To multiply a vector by a scalar, just multiply the similar components, that is, the vector’s magnitude by the scalar’s magnitude.
This will now result in a new vector that has the same direction as the vector and is the product of the two magnitudes of the quantities.
For example,
Let us consider the vector $\vec{a}$ and the scalar quantity k,
When we multiply them, we denote them as $k\vec{a}$
Pictorially, if we consider various values of k as 1,2,3, -1, -2
We get,

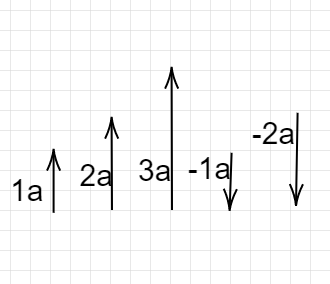
From the above-given set of vectors, we can see that the direction of the vector $\vec{a}$ ,
when the value of the scalar is positive, it remains the same whereas,
when the value of the scalar is negative, the direction becomes exactly opposite.

Note: If we have a vector of type, $\vec{a}=2\hat{i}+\hat{j}+5\hat{k}$ and the scalar quantity which we have to multiply is $3$ then,
$\Rightarrow 3\vec{a}=3\left( 2\hat{i}+\hat{j}+5\hat{k} \right)$
On opening the brackets and multiplying the contents in them we get,
$\Rightarrow 3\vec{a}=6\hat{i}+3\hat{j}+15\hat{k}$
Just multiply the coefficients or the magnitudes.