Question

How do I graph the function of $r = \sin 3\theta$ ?

Answer 1

Hint : Here in this question, we have to plot the graph of the given trigonometric equation. To plot the graph first we have to find the coordinate $\left( {r,\theta } \right)$ by comparing the general equation of the rose curve i.e., $r = a\sin 3\theta$ . By finding the coordinate we can plot the required graph of given trigonometric equation

Complete step-by-step answer :
In general let us consider $r = a\sin (n\theta )$ or $r = a\sin (n\theta )$ where $a \ne 0$ and n is a positive number greater than 1. For the graph of rose if the value of n is odd then rose will have n petals or if the value of n is even then the rose will have 2n petals. Here “a” represents the radius of the circle where the rose petals lie.
Now consider the given equation $r = \sin 3\theta$ . Here a=1, the radius of the circle is 1 and n=3, the number is odd so we have 3 petals for the rose.
Now consider the given equation $r = \sin (3\theta )$ ------- (1)
Substitute r=0 in equation (1) we have
$\Rightarrow 0 = \sin (3\theta )$
By taking the inverse we have
$\Rightarrow {\sin ^{ - 1}}(0) = 3\theta$
By the table of trigonometry ratios for standard angles in radians we have $\sin \left( {n\pi } \right) = 0$ , but here n = 1 so we have
$\Rightarrow \pi = 3\theta$
Dividing by 3 on the both sides we have
$\Rightarrow \theta = \dfrac{\pi }{3}$
Therefore $\left( {\alpha ,\beta } \right) = \left( {r,\theta } \right) = \left( {0,\dfrac{\pi }{3}} \right)$
While determining the area we use the above coordinates
Hence the graph of the given rose curve equation $r = \sin 3\theta$ is:

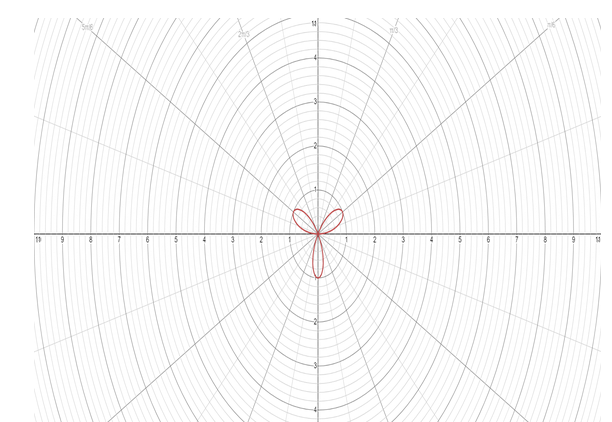
Note : Here we have to plot the polar graph. The polar graph is plotted versus $r$ and $\theta$ . By substituting the value of $\theta$ we can determine the value of $r$ . Here a=1, the radius of the circle is 1 and n=3, the number is odd so we have 3 petals for the rose. The petals will not exceed the circle of radius