Question

How do I graph $\dfrac{{{{(y + 3)}^2}}}{{25}} - \dfrac{{{{(x + 2)}^2}}}{{16}} = 1$ algebraically?

Answer 1

Hint : The given algebraic equation is the equation of the conic section known as hyperbola. We will now compare the equation of hyperbola with the standard equation of hyperbola then find its different properties which will help to plot it, those properties are the center of the hyperbola and the other one is the vertices of the hyperbolas. The standard equation is
$\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} - \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$ or
$\dfrac{{{{(y - k)}^2}}}{{{a^2}}} - \dfrac{{{{(x - h)}^2}}}{{{b^2}}} = 1$ ,for horizontal and vertical hyperbola respectively. Since we are given vertical hyperbola (we know this from seeing that our equation is identical to the second equation we will calculate centre as $(h,k)$ and the equation of vertices will be $\left( {h,k \pm a} \right)$ .

Complete step-by-step answer :
Given $\dfrac{{{{(y + 3)}^2}}}{{25}} - \dfrac{{{{(x + 2)}^2}}}{{16}} = 1$ is the equation of the hyperbola. On comparing with the standard equation we can know the center of the hyperbola which is $(h,k)$ and the vertices by the formula $\left( {h,k \pm a} \right)$ after comparing from the standard equation which is given as follows:
$\dfrac{{{{(y - k)}^2}}}{{{a^2}}} - \dfrac{{{{(x - h)}^2}}}{{{b^2}}} = 1$ on comparing with the original equation we get
$h = - 2,{\text{ }}k = - 3,a = 5,b = 4$
Now according to the above formula for centre of the hyperbola we can write that center is
$( - 2, - 3)$
The values of the vertices is given by the formula $\left( {h,k \pm a} \right)$ by applying the above formula we get
The value of two vertices as ( $- 2,2)$ and $( - 2,8)$ . Now we will plot the points and get our hyperbola plotted on the two dimensional coordinate plane as

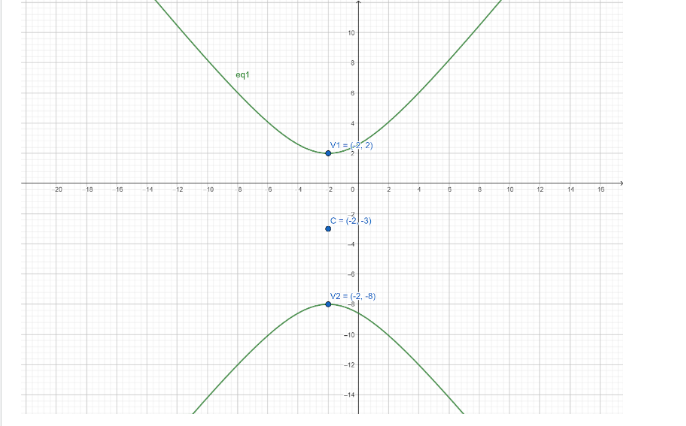
Here C and V $1$ and V $2$ are the centre, and vertices respectively.

Note : The hyperbolas are of two types one is normal hyperbola which can be either horizontal or vertical and the other type is the rectangular hyperbola. This occurs when the semimajor and semiminor axes are equal.