Question

How do I graph cardioid $r=a\left( 1-\cos \theta \right)$?

Answer 1

We will use polar coordinates concept to draw the graph. Here we have to generate the table for different known values of $\theta$ to find r. As we already know that the polar coordinate graph will contain points as $(r,\theta )$ we will plot the graph. The value of $a$ can be any random variable.

Complete step by step answer:
Before going to draw the graph lets know about cardioids.
A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion
For horizontal cardioid the equation will look like
$r=a\pm a\cos \theta$
For vertical cardioid the equation will be like
$r=a\pm a\sin \theta$
Given equation is
$r=a\left( 1-\cos \theta \right)$
We can see it is in the form of a horizontal equation. So we will get a horizontal cardioid from our equation.
So to plot a graph first we have to create a table for the values $(r,\theta )$ .
For this we will take the $\theta$ values in the range between $0$ and $2\pi$.
$0\le \theta <2\pi$
So now will find $r$ values for these $\theta$ values $0,\dfrac{\pi }{2},\pi ,\dfrac{3\pi }{2},2\pi$.
To draw the graph let us assume value of a as $2$

$\theta$	$r=a\left( 1-\cos \theta \right)$
$0$	$0$
$\dfrac{\pi }{2}$	$2$
$\pi$	$4$
$\dfrac{3\pi }{2}$	$2$
$2\pi$	$0$

So using these values we can draw the graph of the given equation.
The graph that obtained is

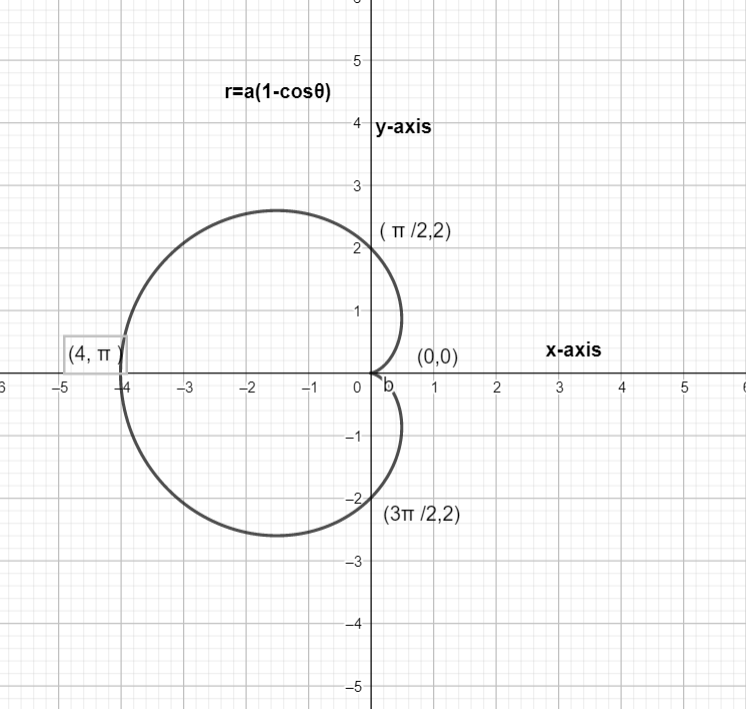
This is the cardioid graph of the equation $r=a\left( 1-\cos \theta \right)$.

Note: We can see the change in the area and perimeter of the graph by changing the values of $a$. We can find area, perimeter, arc length and tangential angle. But if the value of $a$ we have chosen is not a circle radius then the envelope formed is a limacon.