Question

How do I find the value of $\sec \left( -{{240}^{\circ }} \right)$ ?

Answer 1

Here in this question, first write the $\sec \left( -{{240}^{\circ }} \right)$ using reciprocal identities. Then convert the degrees to radians. After conversion, we have to use the trigonometric identities to solve the function. We will apply cos(x + y) = cosx.cosy – sinx.siny for further calculations. After that we will use trigonometric ratios to find the values for angles.

Complete step by step answer:
Now, let’s solve the question.
As we all know the basic functions and derived functions. Derived functions are obtained from basic functions itself. So, first we will write all of them.
$\Rightarrow$ Sine (sin)
$\Rightarrow$Cosine (cos)
$\Rightarrow$Tangent (tan)
$\Rightarrow$cosec$\theta$ = $\dfrac{1}{\sin \theta }$
$\Rightarrow$sec$\theta$ = $\dfrac{1}{\cos \theta }$
$\Rightarrow$tan$\theta$ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow$cot$\theta$ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
Where $\theta$ means angle in degrees or radians.

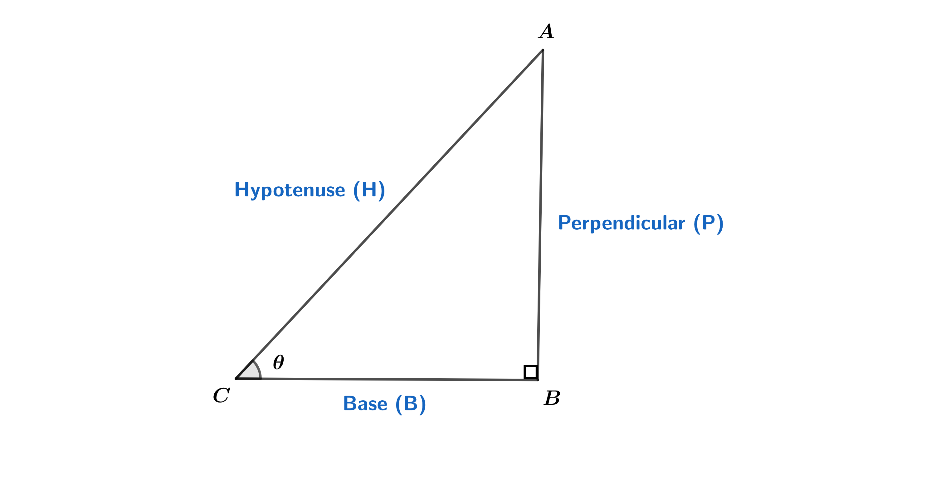
This is the right-angled triangle with an angle $\theta$ at C.
We can find different functions using this triangle. Let’s say we want to find cos$\theta$, then the value of cos$\theta$ will be:
$\Rightarrow$cos$\theta$ = $\dfrac{base(B)}{hypotenuse(H)}$
But if we want for sec$\theta$, we will reciprocate cos$\theta$, so:
$\Rightarrow$sec$\theta$ = $\dfrac{hypotenuse(H)}{base(B)}$
Let’s study some of the trigonometric ratios from the below table:

Trigonometric ratios(angle $\theta$ in radians)	0	$\dfrac{\pi }{6}$	$\dfrac{\pi }{4}$	$\dfrac{\pi }{3}$	$\dfrac{\pi }{2}$
sin$\theta$	0	$\dfrac{1}{2}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{\sqrt{3}}{2}$	1
cos$\theta$	1	$\dfrac{\sqrt{3}}{2}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{1}{2}$	0
tan$\theta$	0	$\dfrac{1}{\sqrt{3}}$	1	$\sqrt{3}$	$\infty$
cosec$\theta$	$\infty$	2	$\sqrt{2}$	$\dfrac{2}{\sqrt{3}}$	1
sec$\theta$	1	$\dfrac{2}{\sqrt{3}}$	$\sqrt{2}$	2	$\infty$
cot$\theta$	$\infty$	$\sqrt{3}$	1	$\dfrac{1}{\sqrt{3}}$	0

We can also obtain some values by reciprocating the functions:
$\Rightarrow$sinx = $\dfrac{1}{\cos ecx}$ or cosecx = $\dfrac{1}{\sin x}$
$\Rightarrow$cosx = $\dfrac{1}{\sec x}$ or secx = $\dfrac{1}{\cos x}$
$\Rightarrow$tanx = $\dfrac{1}{\cot x}$ or cotx = $\dfrac{1}{\tan x}$
Now, let’s see some even and odd functions.
$\Rightarrow$sin(-x) = -sinx
$\Rightarrow$ cos(-x) = cosx
$\Rightarrow$ tan(-x) = -tanx
$\Rightarrow$ cot(-x) = -cotx
$\Rightarrow$ cosec(-x) = -cosecx
$\Rightarrow$sec(-x) = secx
Write the function given in the question.
$\Rightarrow \sec \left( -{{240}^{\circ }} \right)$
As sec(-x) = secx, so:
$\Rightarrow \sec \left( -{{240}^{\circ }} \right)$ = $\sec \left( {{240}^{\circ }} \right)$
We have to apply reciprocal identity to convert in terms of cos.
$\Rightarrow \dfrac{1}{\cos \left( {{240}^{\circ }} \right)}$
Now we have to convert the given degrees to radians.
As we know that one revolution of a circle is of ${{360}^{\circ }}$ which is equal to $2\pi$ radians.
$\Rightarrow {{360}^{\circ }}=2\pi$radians
Now if ${{360}^{\circ }}=2\pi$ radians and if we will divide both sides by 2, we get:
$\Rightarrow \dfrac{{{360}^{\circ }}}{2}=\dfrac{2\pi }{2}$
After reducing the terms, we will get:
$\Rightarrow {{180}^{\circ }}=\pi$ Radians
So, this is the conversion from degrees to radians. If we wish to convert any degree into radian, we have to multiply the degree with a factor of $\dfrac{\pi }{{{180}^{\circ }}}$.
For ${{240}^{\circ }}$, we will multiply it by $\dfrac{\pi }{{{180}^{\circ }}}$ to obtain in radians.
$\Rightarrow {{240}^{\circ }}\times \dfrac{\pi }{{{180}^{\circ }}}$
On reducing the terms, we will get the value $\dfrac{4\pi }{3}$ radians.
So now it will be:
$\Rightarrow \dfrac{1}{\cos \left( \dfrac{4\pi }{3} \right)}$
Can we write $\dfrac{4\pi }{3}$ as $\left( \pi +\dfrac{\pi }{3} \right)$. Place this in above expression:
$\Rightarrow \dfrac{1}{\cos \left( \pi +\dfrac{\pi }{3} \right)}$
After this, we will use sum and difference identities so solve further. The sum identity is:
$\Rightarrow$cos(x + y) = cosx.cosy – sinx.siny
Here, x = $\pi$ and y = $\dfrac{\pi }{3}$. Place the angles in the formula, we will get:
$\Rightarrow \dfrac{1}{\left( \cos \pi .\cos \dfrac{\pi }{3}-\sin \pi .\sin \dfrac{\pi }{3} \right)}$
cos$\dfrac{\pi }{3}$ and sin$\dfrac{\pi }{3}$ are given in trigonometric ratios table, and cos$\pi$ = -1 and sin$\pi$ = 0. Place all the values:
$\Rightarrow \dfrac{1}{\left( (-1).\dfrac{1}{2}-0.\sin \dfrac{\sqrt{3}}{2} \right)}$
After calculation we will get:
$\Rightarrow \dfrac{1}{\left( \dfrac{-1}{2} \right)}$
After reciprocating:
$\Rightarrow \sec \left( -{{240}^{\circ }} \right)$ = -2
This is the final answer.

Note:
There is no direct trigonometric ratio for $\sec \left( -{{240}^{\circ }} \right)$, that’s why we first reciprocated and then split the angles so that it becomes easier to find the value. All the trigonometric identities should be on the tips for solving any questions related to angles, equations or simplification of the expression.