Question

How do I find the standard equation of a circle with centre $\left( 3,6 \right)$ and pass through the point $\left( -1,4 \right)$ ?

Answer 1

For this problem, we translate the coordinate axes to the point $\left( 3,6 \right)$ and then carry out the derivation of the equation of the circle just like we do for a circle with origin as its centre. At the end, we substitute the original previous coordinate system values.

Complete step by step solution:
The standard equation of a circle is
${{x}^{2}}+{{y}^{2}}={{a}^{2}}$
Where, $a$ is the radius of the circle. The circle for the above equation has its centre at the origin. But we can also solve for the equation of a circle which does not have its centre at the origin. This can be done by translating the origin without rotation to the new centre.
The given centre is $\left( 3,6 \right)$ . So, we need to translate the coordinate system to the point $\left( 3,6 \right)$ . Let the previous coordinate system be denoted by $x-y$ and the new coordinate system by $x'-y'$ . The relation between the two coordinate systems will then be,
$x'=x-3$ and $y'=y-6$ ……equation $\left( 1 \right)$

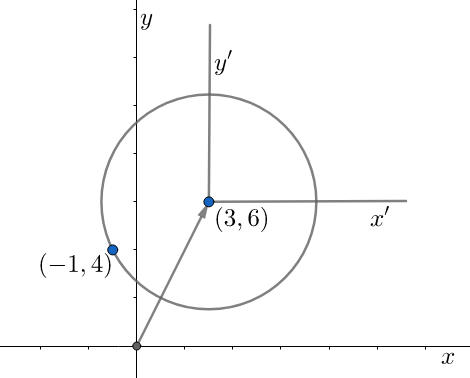
The radius of the circle will be the distance between the centre of the circle, that is $\left( 3,6 \right)$ and the point lying on the circle, that is $\left( -1,4 \right)$ . The distance between the two point will be,
$\sqrt{{{\left( 3+1 \right)}^{2}}+{{\left( 6-4 \right)}^{2}}}=\sqrt{16+4}=\sqrt{20}$
Thus, the equation of the circle according to the coordinate system $x'-y'$ will then be,
$\begin{aligned} & \Rightarrow {{\left( x' \right)}^{2}}+{{\left( y' \right)}^{2}}={{\left( \sqrt{20} \right)}^{2}} \\\ & \Rightarrow {{\left( x' \right)}^{2}}+{{\left( y' \right)}^{2}}=20 \\\ \end{aligned}$
But, we need to write the equation according to the $x-y$ coordinate system. So, we need to replace $x',y'$ with $x,y$ respectively. This can be done using the equation $\left( 1 \right)$ . So, substituting the values in the equation, we get,
$\Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-6 \right)}^{2}}=20$
Therefore, we can conclude that the standard equation of a circle with centre $\left( 3,6 \right)$ and passes through the point $\left( -1,4 \right)$ is ${{\left( x-3 \right)}^{2}}+{{\left( y-6 \right)}^{2}}=20$.

Note: We should be careful while translating the axes and should develop the relations between the coordinate systems correctly. At last, we should also check whether the equation derived is correct by putting the point in the equation and checking if it gets $0$ . Generally, for a circle with centre $\left( a,b \right)$ as centre and radius $r$ , the standard equation will be ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ .