Solveeit Logo
Login

Question

Question: How do I find the slope of the line which passes through the points (-2,3) and (-4,5)?...

How do I find the slope of the line which passes through the points (-2,3) and (-4,5)?

Explanation

Solution

We are given two points as (-2,3) and (-4,5). We are asked to find the slope of the line which passes through these points. To answer this, we will learn what slope of line means, then we will focus on the various methods, we will learn about slope using relation of coordinate, slope-intercept form, then we will use our given points (-2,3) and (-4,5) as (x1,y1),(x2,y2)\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right) to find our slope.

Complete step by step solution:
We are given two points as (-2,3) and (-4,5). We have to find the slope of the line passing through these points. To do so, we will understand what is a slope, and will focus on ways to find the slope.
Now, we have two points (-2,3) and (-4,5), we start by considering the first point (x1,y1)=(−2,3)\left( {{x}_{1}},{{y}_{1}} \right)=\left( -2,3 \right) and the other point as (x2,y2)=(−4,5)\left( {{x}_{2}},{{y}_{2}} \right)=\left( -4,5 \right).
Now, we will use, slope=sin⁡cos⁡slope=\dfrac{\sin }{\cos }
Now, the slope of any line is the angle made by the line with the positive x-axis. We generally find the slope by finding the ratio of rise and run.
Rise means movement of the function along the y-axis while run refers to the movement along the x-axis.
So, one way is slope = riserun\dfrac{rise}{run}.
Another way is to find tan of the angle made by the line with x-axis.
So, slope = tan⁡θ\tan \theta .

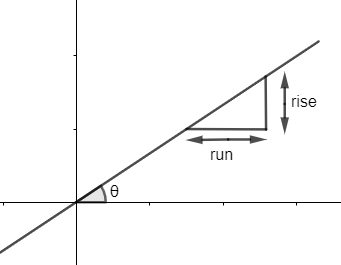
Slope is denoted as m, so we can write,
m=tan⁡θm=\tan \theta or m=riserunm=\dfrac{rise}{run}
Another way to find the slope is to use the equation of line.
General equation of line in standard form is given as ax+ by+ c =0.
We can convert this equation to slope intercept form, that is, y = mx+ c and get the slope and the intercept from there.
Now, we have two points (-2,3) and (-4,5). We will start by considering the first point (x1,y1)=(−2,3)\left( {{x}_{1}},{{y}_{1}} \right)=\left( -2,3 \right) and the other point as (x2,y2)=(−4,5)\left( {{x}_{2}},{{y}_{2}} \right)=\left( -4,5 \right).
Now, we will use, slope=sin⁡cos⁡slope=\dfrac{\sin }{\cos }.
Run is the difference in x-interval, so we can write,
run=x2−x1run={{x}_{2}}-{{x}_{1}}
We know that x1=−2,x2=−4{{x}_{1}}=-2,{{x}_{2}}=-4. So, we get,
run=x2−x1 ⇒−4−(−2) ⇒−4+2 ⇒−2 \begin{aligned} & run={{x}_{2}}-{{x}_{1}} \\\ & \Rightarrow -4-\left( -2 \right) \\\ & \Rightarrow -4+2 \\\ & \Rightarrow -2 \\\ \end{aligned}
Rise is the difference in the y-interval, so we can write,
rise=y2−y1rise={{y}_{2}}-{{y}_{1}}
We know that y1=3,y2=−5{{y}_{1}}=3,{{y}_{2}}=-5. So, we get,
rise=y2−y1 ⇒(5)−3 ⇒5−3 ⇒2 \begin{aligned} & rise={{y}_{2}}-{{y}_{1}} \\\ & \Rightarrow \left( 5 \right)-3 \\\ & \Rightarrow 5-3 \\\ & \Rightarrow 2 \\\ \end{aligned}
Hence, we have got rise = 2 and run = -2. So, on substituting these in the formula of slope, we will get,
slope=riserun=2−2=−1slope=\dfrac{rise}{run}=\dfrac{2}{-2}=-1
Therefore, we got the slope as -1.

Note: We can also use the formula, slope=y2−y1x2−x1slope=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}.
Here, we had assumed (x1,y1)=(−2,3)\left( {{x}_{1}},{{y}_{1}} \right)=\left( -2,3 \right) and (x2,y2)=(−4,5)\left( {{x}_{2}},{{y}_{2}} \right)=\left( -4,5 \right).
So, we get,
slope=5−3−4−(−2)=2−2=−1slope=\dfrac{5-3}{-4-\left( -2 \right)}=\dfrac{2}{-2}=-1
In case we have the equation of the line as ax+ by +c=0, then we could have found the slope using the formula, m=−abm=\dfrac{-a}{b}.