Question

How do I find the range of the function $y = - {2^x} + 2$?

Answer 1

We have to determine the range of the given function. For this, put $y = f\left( x \right)$ and solve the equation $y = f\left( x \right)$ for $x$ in terms of $y$. Next, put $x = \phi \left( y \right)$ and find the values of $y$ for which the values of $x$, obtained from $x = \phi \left( y \right)$, are real and in the domain of $f$. Thus, the set of values of $y$ obtained is the range of $f$.

Complete step by step solution:
Given function: $y = - {2^x} + 2$
We have to find the range of a given function.
For this, put $y = f\left( x \right)$ and solve the equation $y = f\left( x \right)$ for $x$ in terms of $y$.
$\Rightarrow y = - {2^x} + 2$
It can be written as ${2^x} = 2 - y$
Take logarithm both sides of the equation, we get
$\Rightarrow \ln \left( {{2^x}} \right) = \ln \left( {2 - y} \right)$
Use property $\ln \left( {{a^m}} \right) = m\ln \left( a \right)$, we get
$\Rightarrow x\ln \left( 2 \right) = \ln \left( {2 - y} \right)$
Now, put $x = \phi \left( y \right)$ and find the values of $y$ for which the values of $x$, obtained from $x = \phi \left( y \right)$, are real and in the domain of $f$.
$2 - y > 0$
$\Rightarrow y < 2$
Clearly, Range ($f$) $= \left( { - \infty ,2} \right)$.

Therefore, the range of given function is $\left( { - \infty ,2} \right)$.

Note: In above question, we can determine the range of a given question by simply drawing the graph of the function.

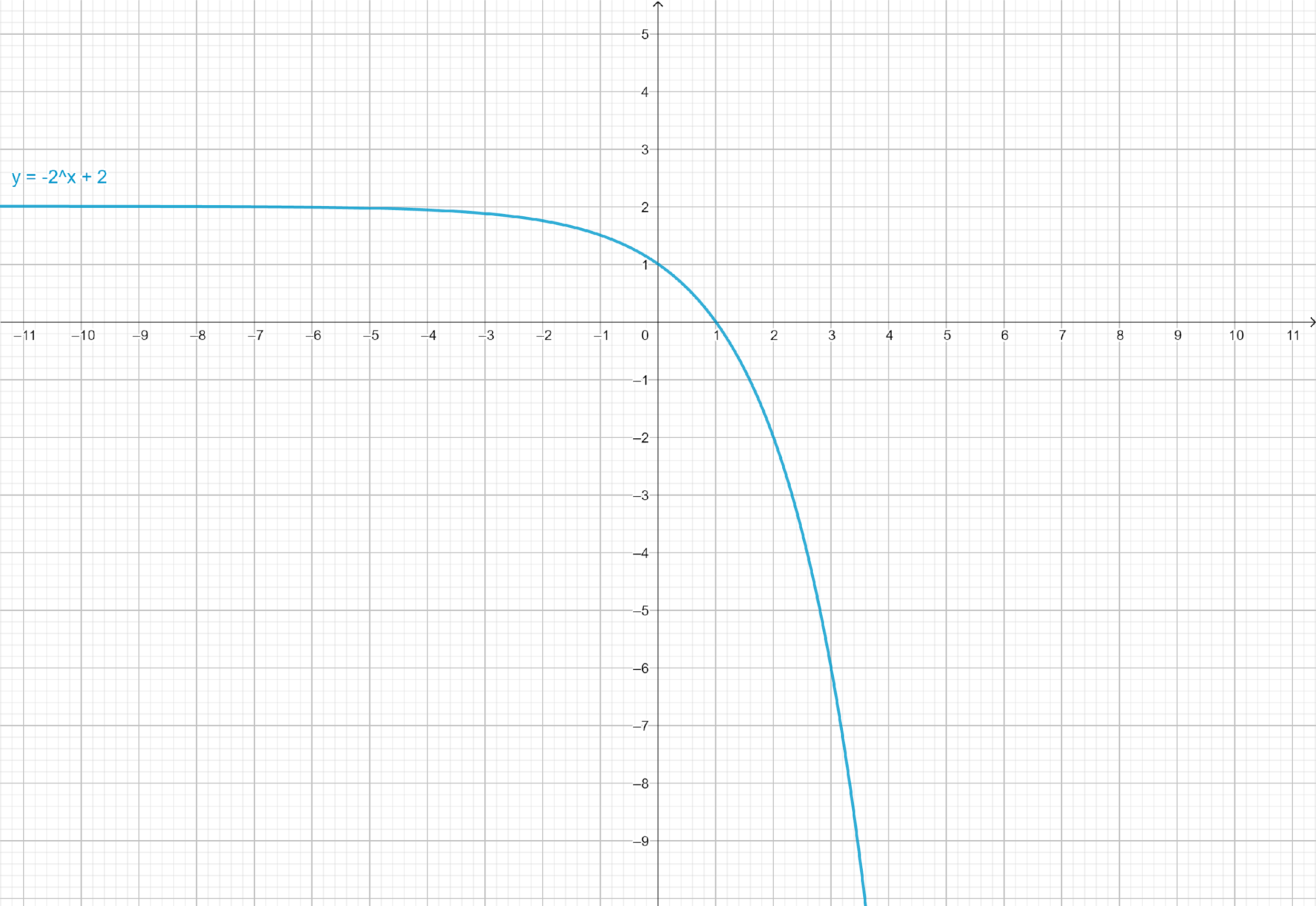
From the graph, we can observe that $y < 2$ for all values of $x$.
Therefore, the range of the given function is $\left( { - \infty ,2} \right)$.