Question

How do I find the orthogonal projection of two vectors?

Answer 1

Orthogonal projection between two vectors states that the angle between these two vectors is ${90^ \circ }$.
We will put this value into the general formula to find the value of projection.

Formula used: If two vectors $\overrightarrow a$, $\overrightarrow b$ are there in a $2D - plane$, and they make an angle of $\theta$, then we can write the following equation:

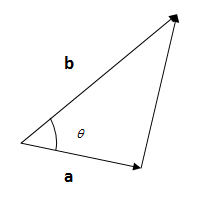
So, The vector projection of $b$ onto $a$: we said that the length of the projection is $\left| b \right|\cos \theta$.
So, $\left| a \right|\left| b \right|\cos \theta = ab$.
So, it is written as $pro{j_a}b$.
We can divide both the sides by $\left| a \right|$ to get the value of $\left| b \right|\cos \theta$.

Complete step-by-step solution:
Let's say, we want to find the projection of $\overrightarrow x$ on another $\overrightarrow y$ in the same vector space.
Also, consider that the projection is denoted by $\overrightarrow p$.
Then we can set the dot product of these two vectors using the above formula:
$\left| {\overrightarrow x } \right|\left| {\overrightarrow {(y - p)} } \right|\cos \theta = \overrightarrow x \overrightarrow {(y - p)}$.
But these two vectors are orthogonal, the angle between them should be equal to ${90^ \circ }$.
So, we can rewrite the above equation in following way:
\Rightarrow$$$\left| {\overrightarrow x } \right|\left| {\overrightarrow {(y - p)} } \right|\cos {90^ \circ } = \overrightarrow x \overrightarrow {(y - p)} $$. We know that the value of $$\cos {90^ \circ } = 0$$, putting it to the above equation, we get: \Rightarrow\overrightarrow x \overrightarrow {(y - p)} = 0$$. Now, using the property of dot product, we get the following equation: $\Rightarrow\overrightarrow x \overrightarrow y - \overrightarrow x \overrightarrow p = 0..........(1)$. Now, as the projection of these two vectors is along the side to$\overrightarrow x , or $\Rightarrow$$$\overrightarrow p is along$\overrightarrow x$, $\overrightarrow p$ would be some multiple of $\overrightarrow x$.
Let say, $\overrightarrow p = m\overrightarrow x$
So, we can rewrite the equation $(1)$ as following:
\Rightarrow$$$\overrightarrow x \overrightarrow y - \overrightarrow x m\overrightarrow x = 0$$ After applying the rules of dot products, we get: \Rightarrow$$$\overrightarrow x \overrightarrow y - \overrightarrow x m\overrightarrow x = 0$$

So, the require projection vector $\overrightarrow p$ would be $\dfrac{{\overrightarrow x \overrightarrow y }}{{\left| x \right|\left| x \right|}}\overrightarrow x$.

Note: Vector projection is the vector produced when one vector is resolved into two component vectors.
One vector is perpendicular to the second vector and the other one is parallel to the second vector.
The parallel one is called a projection vector.