Question

How do I find the ${{n}^{th}}$ power of a complex number?

Answer 1

We can find the ${{n}^{th}}$ power of a complex number by using the complex number in a rectangular form and we have to do some more process to get the ${{n}^{th}}$ power of a complex number.

Complete step by step answer:
Now considering from the question we need to find the ${{n}^{th}}$ power of the complex number.
Let the complex number be $z=a+ib$ .
We could use the complex number in rectangular form $\left( z=a+ib \right)$ and multiply it ${{n}^{th}}$ times by itself but this is not very practical in particular if $n>2$.
What we can do, instead, is to convert the complex number in polar form.
Polar form of the complex number: $z=r\angle \theta$
Where $r$ in the polar form indicates is the modulus and $\theta$ is the argument.
Below we will have the graphical representation to understand the concept very clearly,
Graphical representation:

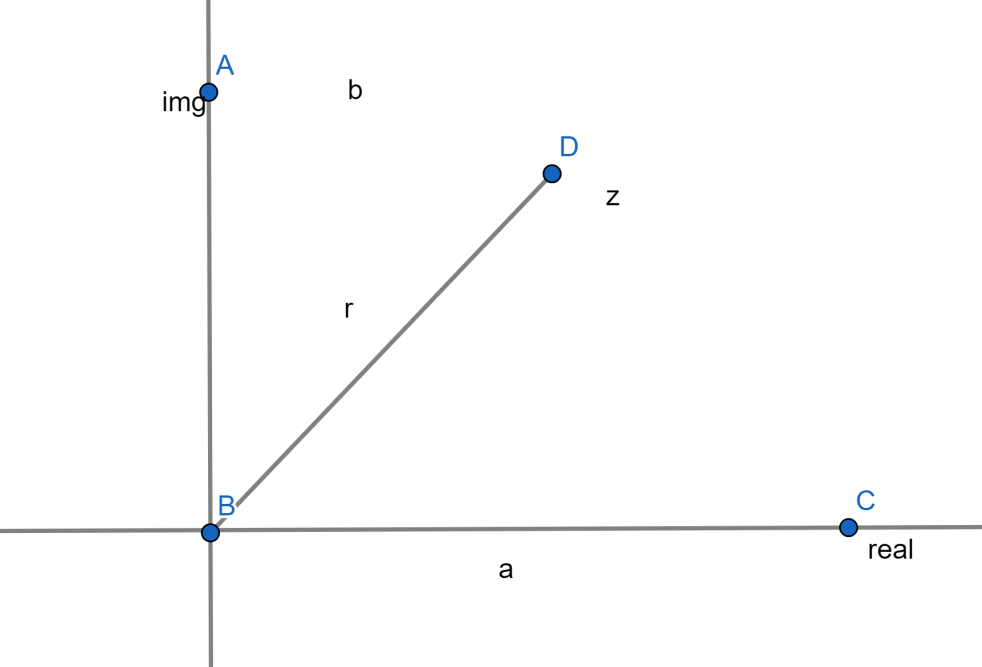
So that now the ${{n}^{th}}$ power becomes as below written,
${{z}^{n}}={{r}^{n}}\angle n.\theta$
We can now wonder what does the rectangular form of the result specify. We get this using the trigonometric form and do some math.
By looking at our first graph we can say that;
$\begin{aligned} & a=r.\cos \theta \\\ & b=r.\sin \theta \\\ \end{aligned}$
The complex number becomes now:
$z=a+ib=r.\cos \theta +r.\sin \theta .i$
Finally from the question it has been asked to find the ${{n}^{th}}$ power of a complex number.

Therefore ${{n}^{th}}$ power of a complex number is ${{z}^{n}}={{r}^{n}}\angle n.\theta$ which we already got above.

Note: We have to be careful while doing this type of complex number problems. We should have the minimum basic graphical knowledge to solve this type of complex numbers questions. Here we have to write the ${{n}^{th}}$ power of a complex number let it be $z=a+ib$ and it’s magnitude $r=\sqrt{{{a}^{2}}+{{b}^{2}}}$ then it can be written as $z=r\left( \cos \theta +i\sin \theta \right)$ where $\theta$ is the angle made by the number in the complex plane. Then ${{z}^{n}}={{r}^{n}}{{\left( \cos \theta +i\sin \theta \right)}^{n}}={{r}^{n}}\left( \cos n\theta +i\sin n\theta \right)$ . This is similar to ${{z}^{n}}={{r}^{n}}\angle n.\theta$