Question
Question: How do I find the inclination \(\theta \) (in degrees and radians) of the lines passing through the ...
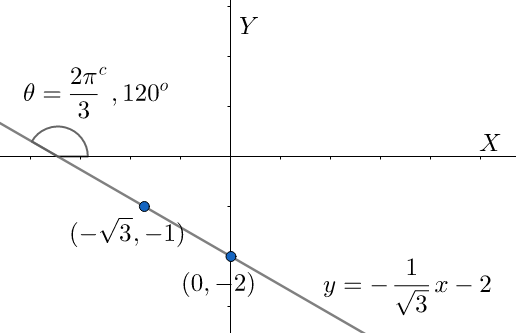
How do I find the inclination θ (in degrees and radians) of the lines passing through the points (−3,−1),(0,−2) ?
Solution
In this problem, we are given two points and we need to find out the inclination of the line passing through it. At first, we find the equation of the line according to y−y1=x2−x1y2−y1(x−x1) . After that, we arrange it in the form y=mx+c and get the slope as −31 , from this the inclination in radians can be found out. The corresponding value in degrees will be by using the formula deg=π180×(rad) .
Complete step-by-step solution:
Given that the two points are (−3,−1),(0,−2) . First, we will determine the equation of the line passing through the points (−3,−1),(0,−2) . The equation of the line passing through the points (x1,y1),(x2,y2) is given by,
y−y1=x2−x1y2−y1(x−x1)
Here, (x1,y1)=(−3,−1)(x2,y2)=(0,−2) . So, the equation of the line passing through (−3,−1),(0,−2) using the above formula is,
⇒y−(−1)=0−(−3)−2−(−1)(x−(−3))⇒y+1=3−1(x+3)⇒3y+3=−x−3⇒y=−31x−2....(i)
The above equation can be compared to the slope intercept form of a straight line. The slope intercept form of a straight line is y=mx+c , where “m” is the slope of the line. Comparing the above line with this form, we get,
m=−31
Now, slope of a line is also given by tanθ , where θ is the inclination of the line. So, we get,
⇒tanθ=−31⇒θ=tan−1(−31)=32π
This is the value of the inclination in radians. To find it in degrees, we use the formula,
deg=π180×(rad)
Using this formula, we get the degree as,
⇒deg=π180×(32π)=120∘
Thus, we can conclude that the inclination of the line is 32π radians and 120∘ .
Note: We can also solve the problem in another way. Instead of derivation the equation first, we can simply find out the inclination as tanθ=x2−x1y2−y1 . Putting the corresponding values, we get, tanθ=0−(−3)−2−(−1)=−31 . Not to mention, we must be careful with the signs as a single mistake can lead to a completely different angle.
