Question

How do I find the equation of hyperbola, given its graph?

Answer 1

The above question is based on finding the equation of hyperbola given in the graph. The main approach towards solving this equation is by understanding the terms and distances between the two curves present in the graph.

Complete step by step solution:
Hyperbola can be defined as a set of points in the coordinate plane. A hyperbola is the set of points in a plane.
Consider the below graph is a graph of hyperbola.

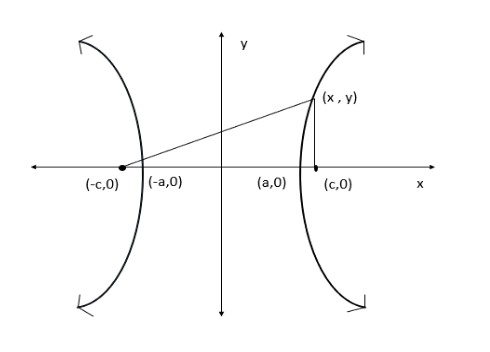
The above graph is an equation of a hyperbola which is centered at the origin. Here the above points (-c,0) and (c,0) are the foci of a hyperbola centered at the origin. The hyperbola is the set of all points (x,y) such that the difference of the distances from (x,y) to the foci is constant. If (a,0) is a vertex , the distance from negative foci to (a,0) is $a - \left( { - c} \right) = a + c$. The distance from (c,0) to (a,0) is $c - a$. The difference between the distances from the foci to the vertex is
$\left( {a + c} \right) - \left( {c + a} \right) = 2a$
Now ${d_2}$ is the distance from $\left( {x,y} \right)$ to $\left( { - c,0} \right)$ and ${d_1}$ is the distance from $\left( {c,0} \right)$ to $\left( {x,y} \right)$.
By definition , $|{d_2} - {d_1}|$ is constant for any point (x,y) on the hyperbola. The standard form of an equation of a hyperbola which is centered at the origin with points $\left( { \pm a,0} \right)$and co- vertices $\left( {0, \pm b} \right)$is
$\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$
Therefore, we get the above equation of hyperbola.
Note: An important thing to note is that the terms $2a$ is the length of the transverse axis, $\left( { \pm a,0} \right)$ are coordinates of vertices and $\left( {0, \pm b} \right)$ are coordinates of co- vertices and length of the conjugate axis given is $2b$.