Question

How do find the midpoint of the segment with endpoints at (-2,-1) and (0,9)?

Answer 1

This type of problem is based on the concept of geometry. First, we have to consider the given endpoints. We then have to use the formula for finding the midpoint, that is, for the endpoints $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ the midpoint (x,y) is $\left( x,y \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$. Here ${{x}_{1}}=-2,{{x}_{2}}=0$ and ${{y}_{1}}=-1,{{y}_{2}}=9$. Substitute these values in the midpoint formula and obtain the value of x and y. Thus, the midpoint of the segment is obtained which is the required answer.

Complete step-by-step answer:
According to the question, we are asked to find the midpoint of the segment with endpoints at (-2,-1) and (0,9).
We have been given the endpoints are (-2,-1) and (0,9)
We know that the formula for midpoint is $\left( x,y \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the endpoints.
Here, x is the coordinate of x-axis and y is the coordinate of y-axis.
Therefore, $x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and $y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$. ---------(1)
Let us now compare this with the given information.
We get $\left( {{x}_{1}},{{y}_{1}} \right)$=(-2,-1) and $\left( {{x}_{2}},{{y}_{2}} \right)$=(0,9).
Therefore, ${{x}_{1}}=-2,{{x}_{2}}=0$ and ${{y}_{1}}=-1,{{y}_{2}}=9$.
Now, let us substitute these values in the formula (1).
First consider x.
We get,
$x=\dfrac{-2+0}{2}$
$\Rightarrow x=\dfrac{-2}{2}$
On further simplifications, we get
$x=-1$
Now consider ‘y’.
We get,
$y=\dfrac{-1+9}{2}$
On further simplifications, we get
$y=\dfrac{8}{2}$
$\therefore y=4$
Therefore, x=-1 and $y=4$.
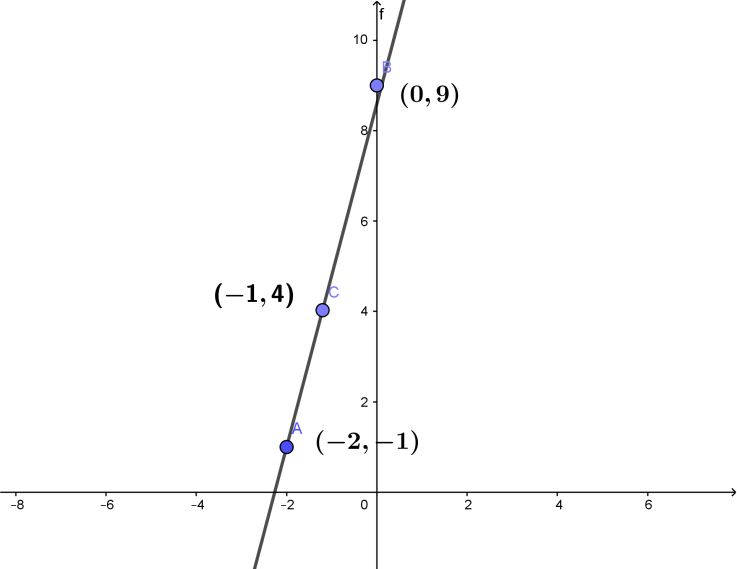
Hence the midpoint of the segment with endpoints at (-2,-1) and (0,9) is (-1,4).

Note: Whenever you get this type of problems, we should always remember the formula for midpoint. We should avoid calculation mistakes based on sign conventions. We should not make calculation mistakes while dividing by 2.we can also plot a graph with the given points to get an idea where the midpoint might lie. Consider A and B to be the end points, that is (-2,-1) and (0,9) respectively. And let C be the midpoint.