Question
Question: How can you find the slope and intercept of \[3y = 7\] ?...
How can you find the slope and intercept of 3y=7 ?
Solution
Since we need to find the slope and intercept so we need to convert the equation into slope-intercept form by solving y and any linear equation has the form of y=mx+c where m stands as slope which can be found by finding two distinct points and c is the y intercept where graph hits y axis.
Formula used:
Since slope m depicts how steep the line is with respect to horizontal. So if in the line two points found are (x1,y1) and (x2,y2) so slope comes out to be
m=x2−x1y2−y1
The point where line crosses why y axis is the y intercept c
Complete step by step solution:
As the given equation is 3y=7
Since we know that y=mx+c is the slope intercept form of a line where m is equal to slope and c is the y intercept (0,c)
Now by dividing both the sides of the equation by 3 we will put the given equation in slope-intercept form.
So they have a slope=0 and this is a horizontal line
It means slope=m=0 and y intercept c=(0,37)
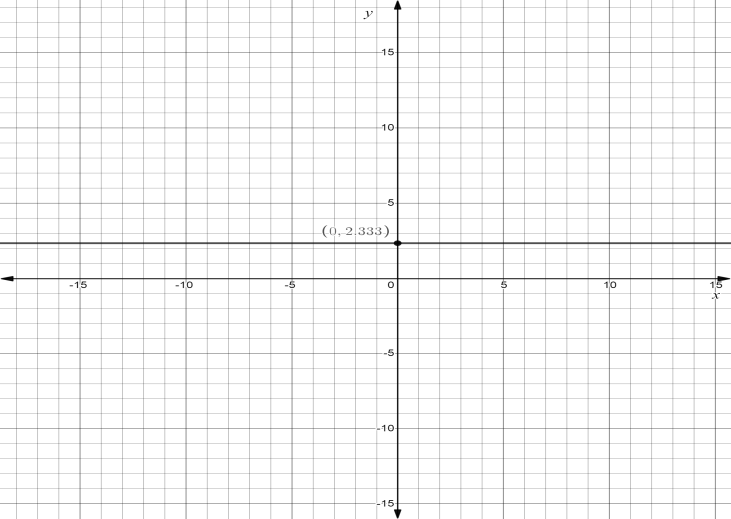
Note: While solving the above equation we need to convert the equation given in the slope intercept form and later on after finding the value of m and c then pick a point on line and check if it satisfies the equation by plugging it in. In the above equation the slope is horizontal as the value of m comes out to be 0. For verification we put value of y in the equation 3y=7 and we found that
It means LHS=RHS.
