Question

How can you find the slope and intercept of $3x + 4y = 16$?

Answer 1

Since we need to find the slope and intercept so we need to convert the equation into slope-intercept form by solving $y$ and any linear equation has the form of $y = mx + c$ where $m$ stands as slope which can be found by finding two distinct points and $c$ is the $y$ intercept where graph hits $y$ axis.

Formula used:
Since slope $m$ depicts how steep the line is with respect to horizontal. So if in the line two points found are $({x_1},{y_1})$ and $({x_2},{y_2})$ so slope comes out to be
$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
The point where line crosses why $y$ axis is the $y$ intercept $c$

Complete step by step solution:
As the given equation is $3x + 4y = 16$
Since we know that $y = mx + c$is the slope intercept form of a line where $m$ is equal to slope and $c$is the $y$intercept
Now we will rearrange the given equation into $y = mx + c$ form in order to calculate value of $m$ and $c$
Hence the equation after isolating $y$ on one side

$$\Rightarrow 4y = - 3x + 16 \\\ \Rightarrow y = - \dfrac{3}{4}x + 4 \\\$$

So we will find that slope is $m = - \dfrac{3}{4}$and $c = 4$
Now we will plot the graph

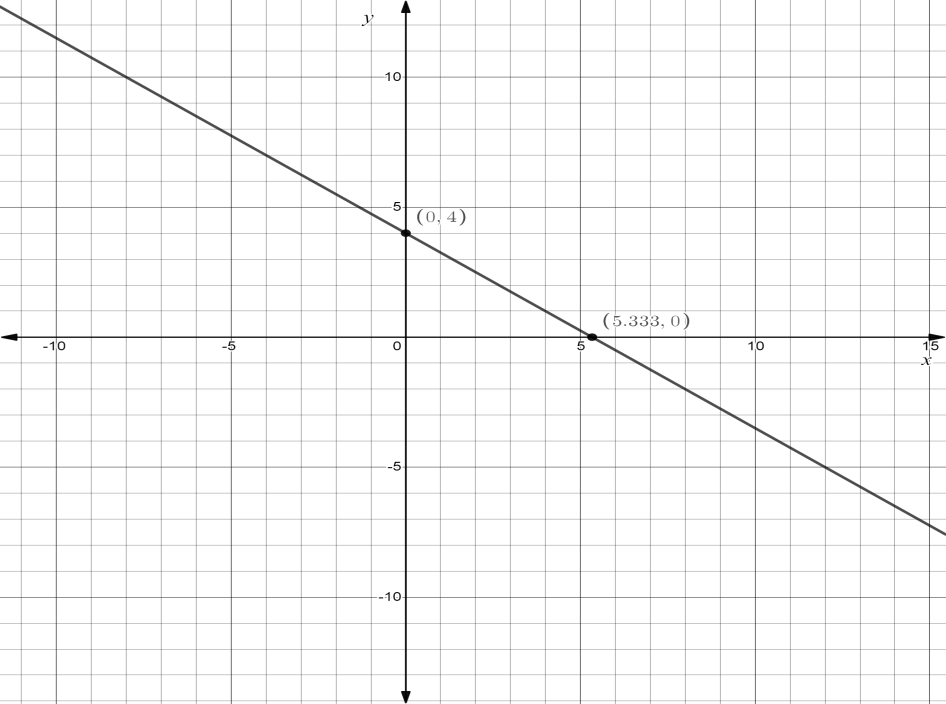
Additional Information:
Keep in mind that slopes can be negative or positive. Here $y$ will tell how far a line goes, $x$ tells us how far along it goes, $m$ tells about the slope and c is the intercept where the lines crosses $y$ axis

Note: While solving the above equation we need to convert the equation given in the slope intercept form and later on after finding the value of $m$ and $c$ then pick a point on line and check if it satisfies the equation by plugging it in. So $x$ intercept is $\left( {\dfrac{{16}}{3},0} \right)$ and $y$ intercept is $(0,4)$ which mean line cuts $y$ axis at $4$