Question

How can three resistors of resistances $2\text{ }\Omega ,3\text{ }\Omega$ and $6\text{ }\Omega$ be connected to give a total resistance of
$\begin{aligned} & (a)\text{ }4\text{ }\Omega \\\ & (b)\text{ }1\text{ }\Omega \\\ \end{aligned}$

Answer 1

For resistances in series, the equivalent resistance will be the sum of each resistances connected in series. For resistances in parallel, the reciprocal of equivalent resistance will be the reciprocal of each of the resistances. Here it is clear that a combination of series and parallel connections can be used to obtain the final solution. This will be helpful in answering this question.

Complete answer:
First of all, let us write the values of resistances given in the question. That is we can write that,
$\begin{aligned} & {{R}_{1}}=2\text{ }\Omega \\\ & {{R}_{2}}=3\text{ }\Omega \\\ & {{R}_{3}}=6\text{ }\Omega \\\ \end{aligned}$
(a)The equivalent resistance of $4\text{ }\Omega$ can be obtained by the following arrangement.

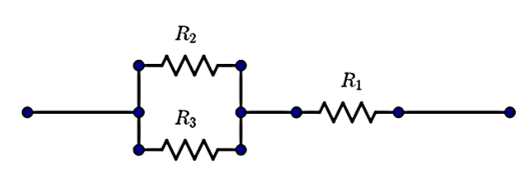
Here, it is a combination of series and parallel resistors. That is we can write that,${{R}_{1}}$ is in series with the parallel combination of ${{R}_{2}}$ and ${{R}_{3}}$. Hence,
${{R}_{1}}+\left[ \dfrac{1}{\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}} \right]={{R}_{eq}}$
Substituting the values of each of the resistances in this equation will give,
$\begin{aligned} & \Rightarrow 2+\left[ \dfrac{1}{\dfrac{1}{3}+\dfrac{1}{6}} \right]={{R}_{eq}} \\\ & \Rightarrow {{R}_{eq}}=2+2 \\\ & \therefore {{R}_{eq}}=4\text{ }\Omega \\\ \end{aligned}$
(b) The equivalent resistance of $1\text{ }\Omega$ can be obtained by connecting the resistances in parallel. Since $1\text{ }\Omega$ is the lowest resistance possible with the given resistors, it can be easily concluded as parallel.
For resistances in parallel, the reciprocal of equivalent resistance will be the reciprocal of each of the resistances.

${{R}_{eq}}=\dfrac{1}{\left( \dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}} \right)}$
Now let us substitute the values in this equation. Substituting the values in the equation will give,$$$$
$\begin{aligned} & \Rightarrow {{R}_{eq}}=\dfrac{1}{\left( \dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6} \right)} \\\ & \Rightarrow {{R}_{eq}}=\dfrac{1}{\left( \dfrac{3}{6}+\dfrac{2}{6}+\dfrac{1}{6} \right)} \\\ & \therefore {{R}_{eq}}=1\text{ }\Omega \\\ \end{aligned}$

Note:
Combinations of resistances are used to achieve a particular resistance in the circuit. In the complex circuits, the various electronics components are having a specific rating for current and voltage, the resistance combinations will maintain the current and potential across these components.