Question

How can the distance formula be derived from the Pythagorean Theorem $?$

Answer 1

We need to know the definition of distance formula and Pythagoras theorem. This question involves the arithmetic operation of addition/ subtraction/ multiplication/ division. We need to know how to find the distance between two points. By using the definition of distance formula and Pythagoras theorem we can easily solve the given question.

Complete step by step answer:
In this question, we would explain how the distance formula be derived from the Pythagoras theorem. Before that, we would explain the Pythagoras theorem and distance formula separately. Let’s see the Pythagoras theorem,

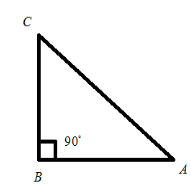
In a rectangular triangle, the square of the hypotenuse side is equal to the sum of the square values of another two sides. This is called Pythagoras theorem.
It can be written as,

AC = \sqrt {A{B^2} + B{C^2}} \\\ $$ Let’s see the distance formula, for this, we take two points as$$\left( {{x_1},{y_1}} \right)$$, $$\left( {{x_2},{y_2}} \right)$$. So, the distance between these two points can be written as, $$d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $$ Let’s see how the distance formula is derived from Pythagoras theorem,  Let’s take$$AB = a$$,$$BC = b$$, and$$CA = c$$. So, the above diagram can be modified as,  Let’s take$$C$$point as$$\left( {{x_1},{y_1}} \right)$$and $$A$$point as$$\left( {{x_2},{y_2}} \right)$$. So the above diagram can be modified as,  From the figure, the distance$$BA$$ can also, be written as$${x_1} - {x_2}$$and $$CB$$can also be written as$${y_1} - {y_2}$$. So, we have  By using Pythagoras theorem, the above diagram can be drawn as,  So, we get $$AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $$$$ \to \left( 6 \right)$$ From the equation $$\left( 1 \right)$$and$$\left( 5 \right)$$, we get how Pythagoras theorem converts into the distance formula as given below.In the equation$$\left( 1 \right)$$, we have the hypotenuse value as $$AC = \sqrt {A{B^2} + B{C^2}} $$.In the equation $$\left( 5 \right)$$, we have the hypotenuse value $$AC = d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $$, by substituting the value of $$AB$$ and $$BC$$ as $$\left( {{x_1} - {x_2}} \right)$$ and $$\left( {{y_1} - {y_2}} \right)$$ respectively. So, the equation may change but the total value of hypotenuse in the equation $$\left( 1 \right)$$ is the same as the value of hypotenuse in the equation $$\left( 5 \right)$$. Here the equation $$\left( 5 \right)$$ is known as the distance formula and the equation $$\left( 1 \right)$$ is known as Pythagorean Theorem. Thus we can prove that the distance formula is derived by the Pythagorean Theorem. This is shown in the equation $$\left( 6 \right)$$. **Note:** In this question, we would involve the arithmetic operations of addition/ subtraction/ multiplication/ division. We would remember the condition for Pythagoras theorem and distance formula. Note that if we want to eliminate squares we can involve the square root. We would consider the point as$$\left( {x,y} \right)$$.