Question

How can I determine whether a horizontal parabola opens to the left or to the right?

Answer 1

A parabola can be horizontal, vertical, or tilted, depending upon the orientation of its axis. In the above question, we have been asked about a horizontal parabola, which means that its axis must be horizontal, that is, parallel to the x-axis. This means that the equation of the parabola must be linear in x and must be of the type ${{y}^{2}}=kx$. The direction of the opening of the parabola will depend on the sign of $k$.

Complete step by step solution:
Since the parabola given in the above question is horizontal, its axis must be parallel to the x-axis. This implies that the equation of the parabola must be linear in x. So we can consider the general equation of a horizontal parabola as
$\Rightarrow {{y}^{2}}=kx$
Now, the direction of the opening of the parabola will depend on the sign of k in the above equation. On the basis of the signs of k, we can have two cases:
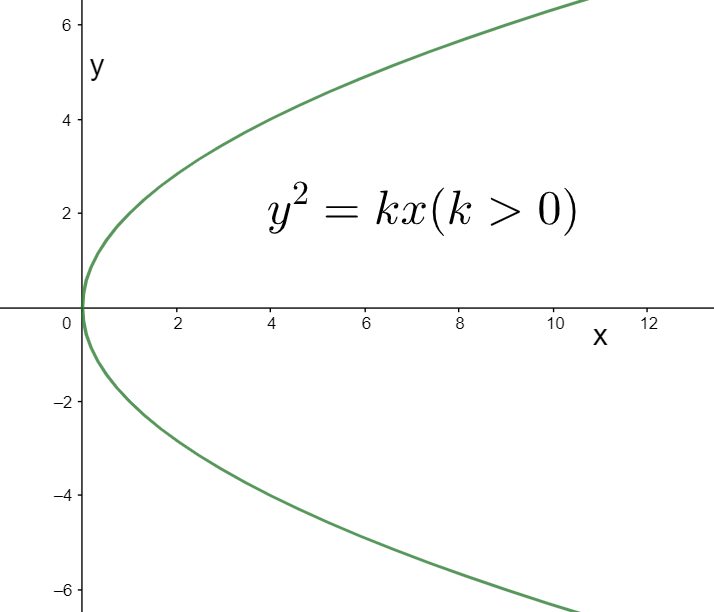
Case I: When k is positive
Considering again the equation of the horizontal parabola, we have
$\Rightarrow {{y}^{2}}=kx$
Since the LHS is equal to the square of y, it must be positive. This implies that the RHS, equal to the product $kx$, must be positive. For this case, we have considered positive value for k. This means that $x$ must also be positive for the product $kx$ to be positive.
Now, we know that the region $x>0$ lies to the right of the origin.
This means that the parabola must open to the right for $k>0$, as shown below.

Case II: When k is negative
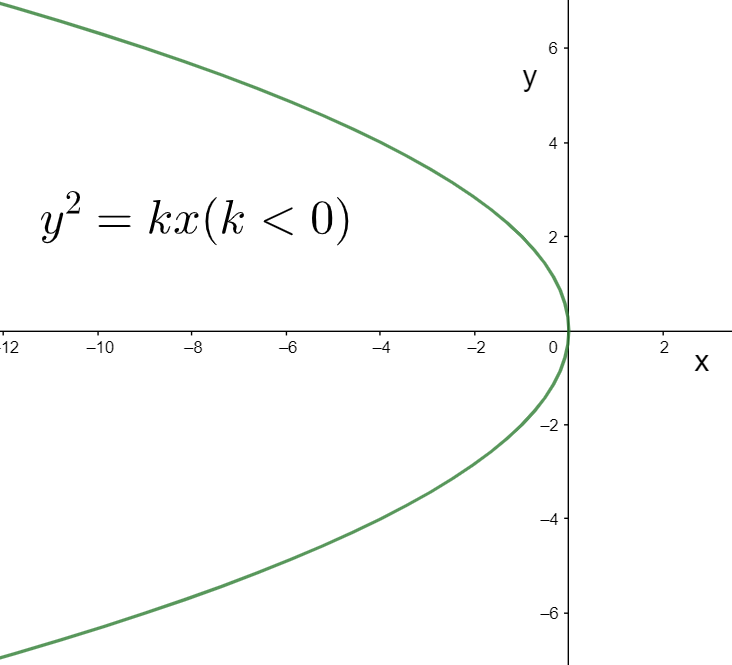
The parabolic equation is
$\Rightarrow {{y}^{2}}=kx$
In this case, the value of $k$ is negative, and since the product $kx$ must be positive, as shown in the above case, the value of $x$ must be negative.
We know that the region $x<0$ lies to the left to the origin.
This means that the parabola must open to the left for $k<0$, as shown below.

Hence, the parabola will open to the left when $k<0$ and to the right when $k>0$.

Note: We must note that before deciding the direction of opening, it is necessary to write the equation of the parabola in the standard form of ${{y}^{2}}=kx$. Then the sign of the coefficient of x will decide the direction of its opening, according to the caes discussed in the above solution.