Question

How can I determine whether a given graph represents a function?

Answer 1

Consider any examples like the graph of the curves $y=x$ and ${{y}^{2}}=x$ and use the vertical line test to check whether these relations are functions or not. Draw vertical lines, i.e., lines parallel to the y – axis, on the graph. If any of these vertical lines cut the graph of the equation at two points having different y – coordinate values then the relation will not be a function.

Complete step by step answer:
Here, we are asked to determine whether a given graph will represent a function or not. So, let us take some examples to check.
Now, here we are taking two relations: $y=x$ and ${{y}^{2}}=x$ and we have to determine from their graphs whether they are functions or not. Now, a relation can only be a function if for no value of x there are more than one value of y. To check if a relation is a function or not we use the vertical line test. In this method first we draw the graph of the given relation, then we draw vertical lines that are parallel to y – axis. If any one of these vertical lines cuts the graph at more than one point then the relation is not considered as a function.
Now, let us check for the relations $y=x$ and ${{y}^{2}}=x$ one – by – one.
(i) For y = x.
The relation y = x represents a straight line. So, drawing its graph, we have,

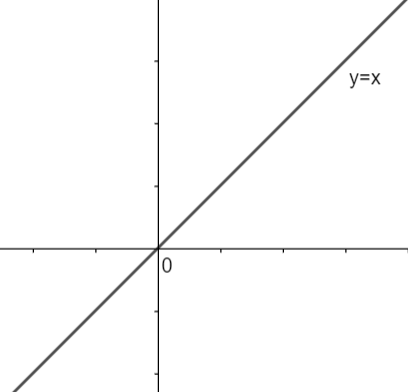
Let us draw some vertical lines on the graph of the above line. So, it will look like:

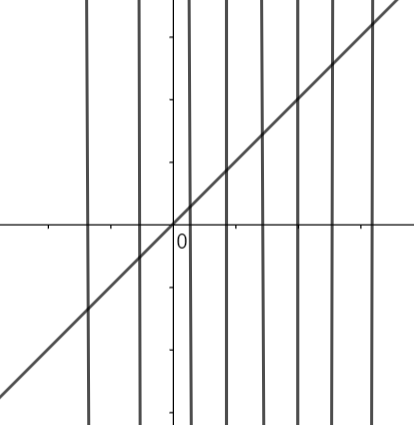
As we can see that there are no lines which are cutting the graph at more than one point. So, for a single value of x there is only one value of y.
Therefore, we can say that the relation y = x is also a function.
(ii) For ${{y}^{2}}=x$.
The relation ${{y}^{2}}=x$ represents a parabola. So, drawing its graph, we have,

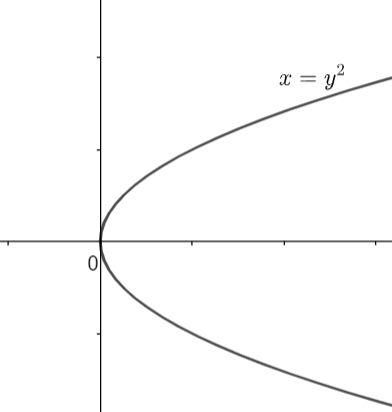
Let us draw some vertical lines on the graph of the above parabola. So, it will look like:

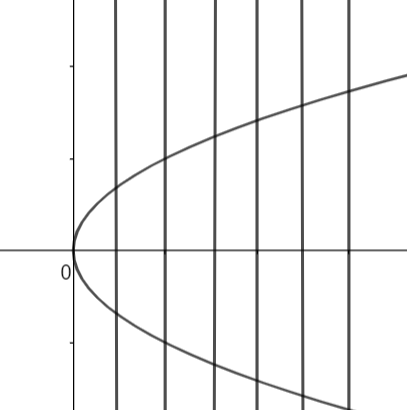
As we can see that there are many lines which are cutting the parabola at more than one point, that is they are cutting the parabola at two points. So, for a single value of x there are two values of y.
Hence, we can conclude that the relation $x={{y}^{2}}$ is not a function.

Note:
One may note that if we have a relation in which we have one value of y for more than one value of x then the relation will be considered as a function. That is called a many – one function. You must remember the vertical line test that we have used to solve the question. Remember the basic differences between a ‘relation’ and a ‘function’ to solve the above question.